Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C F E H
a, Xét \(\Delta AEB\)và \(\Delta AFC\)có :
\(+,\widehat{A}\)chung
\(+,AB=AC\)( \(\Delta ABC\)cân tại A )
\(+,\widehat{ABE}=\widehat{ACE}\left(\widehat{AEB}=\widehat{AFC}=90^0\right)\)
\(\Rightarrow\Delta AEB=\Delta AFC\)
b, \(\Delta AEB=\Delta AFC\left(cmt\right)\)
\(\Rightarrow AF=AE\)
Xét \(\Delta AEH\)và \(\Delta AFH\)có :
\(+,\widehat{AFH}=\widehat{AEH}=90^0\)
\(+,AF=AE\) \(\hept{\begin{cases}\\\Rightarrow\Delta AFH=\Delta\\\end{cases}AEH\left(c.c.c\right)}\)
\(+,AH\)chung
\(\Rightarrow\widehat{FAH}=\widehat{AEH}\)
\(\Rightarrow\)AH là tia phân giác của của góc \(\widehat{A}\)
Mặt khác \(\Delta ABC\)cân tại A
\(\Rightarrow AH\perp BC\)
c, Tự làm nhé ..

Bài 1:Cho góc xOy có Oz là tia phân giác,M là điểm bất kì thuộc tia Oz.Qua M kẻ đường thẳng a vuông góc với Ox tại A cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D.
a,CM tam giác AOM bằng tam giác BOM từ đó suy ra OM là đường trung trực của đoạn thẳng AB
b,Tam giác DMC là tam giác gì?Vì sao?
c,CM DM + AM < DC
Bài 2:Cho tam giác ABC có góc A=90* và đường phân giác BH(H thuộc AC).Kẻ HM vuông góc với BC(M thuộc BC).Gọi N là giao điểm của AB và MH.CM:
a, Tam giác ABGH bằng tam giác MBH.
b, BH là đường trung trực của đoạn thẳng AH
c, AM // CN
d, BH vuông góc với CN
Bài 3:Cho tam giác ABC vuông góc tại C có góc A = 60* và đường phân giác của góc BAC cắt BC tại E.Kẻ EK vuông góc với BK tại K(K thuộc AB).Kẻ BD vuông góc với AE tại D(D thuộc AE).CM:
a, Tam giác ACE bằng tam giác AKE
b, BE là đường trung trực của đoạn thẳng CK
c, KA=KB
d, EB>EC
Bài 4:Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E.Kẻ EH vuông góc BC tại H(H thuộc BC).CM:
a, Tam giác ABE bằng tam giác HBE
b, BE là đường trung trực của đoạn thẳng AH
c, EC > AE
Bài 5:Cho tam giác ABC vuông tại A có đường cao AH
1,Biết AH=4cm,HB=2cm,Hc=8cm:
a,Tính độ dài cạnh AB,AC
b,CM góc B > góc C
2,Giả sử khoảng cách từ điểm A đến đường thẳng chứa cạnh BC là không đổi.Tam giác ABC cần thêm điều kiện gì để khoảng cách BC là nhỏ nhất.
Bài 6:Cho tam giác ABC vuông tại A có đường cao AH.Trên cạnh BC lấy điểm D sao cho BD=BA.
a,CM góc BAD= góc BDA
b,CM góc HAD+góc BDA=góc DAC+góc DAB.Từ đó suy ra AD là tia phân giác của góc HAC
c,Vẽ DK vuông góc AC.Cm AK=AH
d,Cm AB+AC<BC+AH
Bài 7:Cho tam giac ABC vuông tại C.Trên cạnh AB lấy điểm D sao cho AD = AC.kẻ qua D đường thẳng vuông góc với AB cắt BC tại E. AE cắt CD tại I.
a,CM AE là phân giác \{CAB}
b,CM AE là trung trực của CD
c,So sánh CD và BC
d,M là trung điểm của BC,DM cắt BI tại G,CG cắt DB tại K.CM K là trung điểm của DB
Bài 8:Cho tam giác ABC có BC=2AB.Gọi M là trung điểm của BC,N là trung điểm của BM.Trên tia đối của NA lấy điểm E sao cho AN=EN.CM:
a,Tam giác NAB=Tam giác NEM
b,Tam giác MAB là tam giác cân
c,M là trọng tâm của Tam giác AEC
d,AB>\frac{2}{3}AN

a) BD; CE là đường cao => tam giác ABD và tam giác ACE vuông : có: AB = AC (do tam giác ABC cân tại A ); góc A chung
=> tam giác ABD = ACE (cạnh huyền - góc nhọn )
b) Tam giác BDC vuông tại D có trung tuyến DH ứng với cạnh huyền BC => DH = HC = BC/ 2
=> tam giác HDC cân tại H
c) sửa đề: chứng minh: DM = MC
Tam giác DHC cân tại H có HM là đuơng cao nên đông thời là đường trung tuyến => M là TĐ của DC=> DM = MC
d) Tam giác HND vuông tại M có: MI là trung tuyến => MI = HI = HD/2
=> tam giác IHM cân tại I => góc IHM = IMH
lại có HM là p/g của góc DHC => góc IHM = MHC
=> góc IMH = MHC mà 2 góc này ở vị trí SLT => MI // HC mà HC vuông góc với AH
=> MI vuông góc với AH
bạn Nobita Kun giải bài không theo điểm như đề bài cho, ý c đề bài đúng rồi ạ. ý d thì bạn hiểu nhầm đề rồi, bạn xem lại điểm I nhé

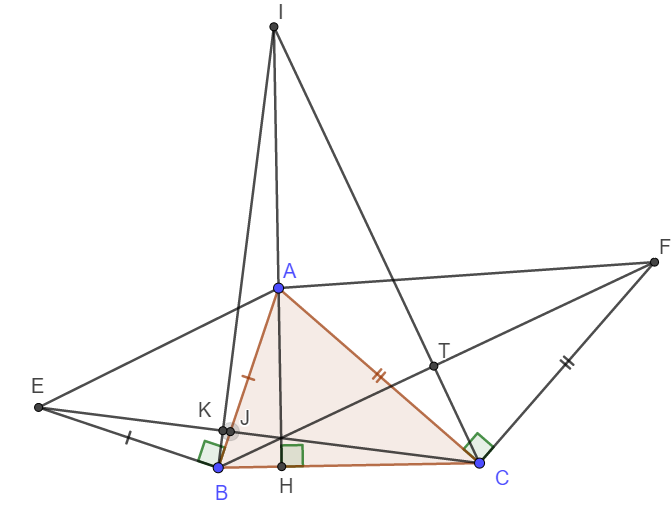
a) Ta có \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
b) Do \(\Delta ABI=\Delta BEC\Rightarrow BI=EC\)
Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
c) Chứng minh hoàn toàn tương tự ta có \(IC\perp BF\)
Gọi giao điểm của IC và BF là T.
Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.
Vậy AH, EC, BF đồng quy tại một điểm.
Vẽ hình đi bạn
Rồi mình giúp bạn làm
Vẽ hình xong gửi tin nhắn cho mình
:) Chúc bạn học tôt
@@

a) Ta có \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
b) Do \(\Delta ABI=\Delta BEC\Rightarrow BI=EC\)
Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
c) Chứng minh hoàn toàn tương tự ta có \(IC\perp BF\)
Gọi giao điểm của IC và BF là T.
Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.
Vậy AH, EC, BF đồng quy tại một điểm.
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔAFH vuông tại F và ΔAEH vuông tại E có
AH chung
AF=AE
Do đó: ΔAFH=ΔAEH
Suy ra: \(\widehat{FAH}=\widehat{EAH}\)
hay AH là tia phân giác của góc BAC
mà ΔABC cân tại A
nên AH là đường cao
Xét tg ABE vuông tại E và tg ACF vuông tại F, có:
AB=AC(tg ABC cân tại A)
góc E=góc F(=90 độ)
góc BAE chung.
=>tg ABE=tg ACF.
b, Xét tg AHF vuông tại F và ΔAEH vuông tại E có
AH chung.
AF=AE(2 cạnh tương ứng)
góc E=góc F.
=>tg AHF=tg AEH.
=>góc FAH=góc EAH.
=>AH là cạnh chung của 2 góc. Vậy AH là tia phân giác của góc BAC.