Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn phải đc k nhiều hơn nx chứ trong 1 ngày bạn ko thể tăng điểm sp đâu


Pt xác định khi:
\(\left\{{}\begin{matrix}5x-4\ge0\\2-x\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{4}{5}\\x\le2\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{4}{5}\le x\le2\)
Nhưng trong TH này cậu phải làm cả hai nhé !
\(\sqrt[]{5x-4}=2-x\)
Phải lấy điều kiện \(2-x\ge0\) vì phương trình trên có dạng :
\(\sqrt[]{A}=B\) nên khi đặt điều kiện \(B\ge0\) thì chắc chắn \(\sqrt[]{A}\ge0\)
Nên không cần điều kiện \(A\ge0\) mà chỉ cần điều kiện \(B\ge0\) hay \(2-x\ge0\) là đủ.

Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.
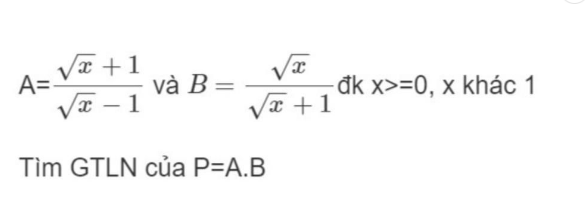

`=10` chứ bn?
vì nó ra kết quả như thế