Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do hạt nhân mẹ Po ban đầu đứng yên, áp dụng định luật bảo toàn động lượng trước và sau phản ứng ta thu được
\(P_{\alpha} = P_{Pb} \)
=> \(2m_{\alpha} K_{\alpha}=2m_{Pb}K_{Pb} \)
=> \( 4,0026.K_{\alpha}=205,9744.K_{Rn}.(1)\)
Áp dụng định luật bảo toàn năng lượng toàn phần có
\(K_{\alpha}+K_{Pb} = (m_t-m_s)c^2\)
=> \(K_{\alpha}+K_{Rn} = (m_{Po}-m_{\alpha}-m_{Pb})c^2= 0,0058.931,5 = 5,4027 MeV. (2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_{\alpha} = 5,2997 MeV; K_{Pb} = 0,103 MeV. \)
=> \(v_{Pb}= \sqrt{\frac{2K_{Pb}}{m_{Pb}}} =\sqrt{\frac{2.0,103.10^6.1,6.10^{-19}}{205,9744.1,66055.10^{-27}}} = 3,06.10^5m/s.\)
Chú ý đổi đơn vị \(1 MeV = 10^6.1,6.10^{-19}J ; 1 u = 1,66055.10^{-27} kg.\)

Cứ mỗi hạt nhân Pôlôni bị phân rã tạo thành 1 hạt nhân chì trong mẫu.
Số hạt nhân Pôlôni bị phân rã là \(\Delta N = N_0 2^{-\frac{t}{T}}.\)
Số hạt nhân Pônôni còn lại là \( N = N_0 2^{-\frac{t}{T}}.\)
Tại thời điểm t1 : \(\frac{\Delta N}{N } = \frac{1-2^{-\frac{t_1}{T}}}{2^{-\frac{t_1}{T}}}= \frac{1}{3}\)
=> \(3(1-2^{-\frac{t_1}{T}})= 2^{-\frac{t_1}{T}}\)
=> \(2^{-\frac{t_1}{T}}= 2^{-2}\)
=> \(t_1 = 2T\)
=> \(t_2 = 2T+276 = 552 \) (ngày)
=> \(\frac{t_2}{T}= \frac{552}{138}= 4.\)
Tại thời điểm t2 : \(\frac{\Delta N_1}{N_1 } = \frac{1-2^{-\frac{t_2}{T}}}{2^{-\frac{t_2}{T}}}= \frac{1-2^{-4}}{2^{-4}}= 15.\)
=> \(\frac{N_1}{\Delta N_1} = \frac{1}{15}.\)

\(_{84}^{210}Po \rightarrow_Z^A X + _2^4He\)
\(m_t-m_s = m_{Po}-(m_X + m_{He}) = 5,805.10^{-3}u > 0\), phản ứng là tỏa năng lượng.
=> \(W_{tỏa} = (m_t-m_s)c^2 = K_s-K_t\)
=> \(5,805.10^{-3}.931,5 = K_X+K_{He}\) (do hạt nhân Po đứng yên nen KPo = Ktruoc = 0)
=> \( K_X+K_{He}=5,4074MeV.(1)\)
Áp dụng định luật bảo toàn động lượng
\(\overrightarrow P_{Po} =\overrightarrow P_{He} + \overrightarrow P_{X} = \overrightarrow 0\)
=> \(P_{He} = P_X\)
=> \(m_{He}.K_{He} =m_X. P_X.(2)\)
Thay mHe= 4,002603 u; mX = 205,974468 u vào (2). Bấm máy giải hệ phương trình được nghiệm
\(K_{He}= 5,3043 \ \ MeV => v_{He} = \sqrt{\frac{2.5,3043.10^6.1,6.10^{-19}}{4,002603.1,66055.10^{-27}}} \approx 1,6.10^7 m/s.\)
mik nghĩ C
nhưng dựa vào định luật bảo tàng động lượng thì xác xuất tỉ lệ chỉ là gần bằng mà thôi nó cũng tương ứng vs 50% còn phải tùy vào sự may mắn hay đáp án nx
mik giải ra là gần bằng 1,6.10^7 m/s

Cứ 1 hạt nhân \(_{92}^{238}U\) bị phân rã tạo ra 1 hạt nhân \(_{82}^{206}Pb\). Từ đó ta có nhận xét là số hạt nhân \(_{92}^{238}U\) bị phân rã chính bằng số hạt nhân \(_{82}^{206}Pb\) tạo thành.
Tỉ số giữa số hạt nhân \(_{92}^{238}U\) bị phân rã và số hạt nhân \(_{92}^{238}U\) còn lại là
\(\frac{\Delta N}{N}= \frac{6,239.10^{18}}{1,188.10^{20}}= 0,0525 = \frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\)
Nhân chéo => \(2^{-\frac{t}{T}}= 0,95.\)
=> \(t = -T\ln_2 0,95 = 3,3.10^8\)(năm)
=> Tuổi của khối đã là 3,3.108 năm.

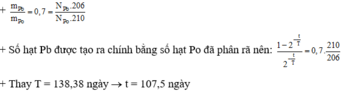

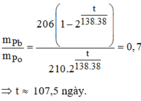

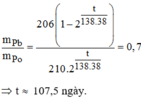

Đáp án A