Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \((C_{15}^{12} + C_{15}^{13} )+ C_{16}^{14} = C_{16}^{13} + C_{16}^{14} = C_{17}^{14} = 680\)

Ta có: \(\sin {70^o} = \cos {20^o};\;\cos {110^o} = - \cos {70^o} = - \sin {20^o}\)
\(\begin{array}{l} \Rightarrow A = {(\sin {20^o} + \cos {20^o})^2} + {(\cos {20^o} - \sin {20^o})^2}\\ = ({\sin ^2}{20^o} + {\cos ^2}{20^o} + 2\sin {20^o}\cos {20^o}) + ({\cos ^2}{20^o} + {\sin ^2}{20^o} - 2\sin {20^o}\cos {20^o})\\ = 2({\sin ^2}{20^o} + {\cos ^2}{20^o})\\ = 2\end{array}\)
Ta có: \(\tan {110^o} = - \tan {70^o} = - \cot {20^o};\;\cot {110^o} = - \cot {70^o} = - \tan {20^o}.\)
\( \Rightarrow B = \tan {20^o} + \cot {20^o} + ( - \cot {20^o}) + ( - \tan {20^o}) = 0\)

a) \(C_4^0 + C_4^1 + C_4^2 + C_4^3 + C_4^4 = {\left( {1 + 1} \right)^4} = {2^4} = 16\)
b) \(C_5^0 - C_5^1 + C_5^2 - C_5^3 + C_5^4 - C_5^5 = {\left( {1 - 1} \right)^5} = {0^5} = 0\)

a) \(C_7^2 = \frac{{7!}}{{2!.5!}} = \frac{{7.6}}{2} = 21\)
b) \(C_9^0 + C_9^9 = \frac{{9!}}{{0!.9!}} + \frac{{9!}}{{9!.0!}} = 2\)
c) \(C_{15}^3 - C_{14}^3 = \frac{{15!}}{{3!.12!}} - \frac{{14!}}{{3!.11!}} = \frac{{15.14.13}}{{3.2.1}} - \frac{{14.13.12}}{{3.2.1}} = 91\)

A = (1- 2) \(\times\) ( 4 - 3) \(\times\) (5 - 6) \(\times\) (8 - 7) \(\times\) (9 - 10) \(\times\) (12 - 11) \(\times\)(13 - 14)
A = (-1) \(\times\) 1 \(\times\) (-1) \(\times\) 1 \(\times\) (-1) \(\times\) 1 \(\times\) (-1)
A = 1

a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {0^o} = 1;\;\cos {120^o} = - \frac{1}{2}\)
Lại có: \(\cos {140^o} = - \cos \left( {{{180}^o} - {{40}^o}} \right) = - \cos {40^o}\)
\(\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { - \frac{1}{2}} \right) - \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0\)
Lại có: \(\sin {175^o} = \sin \left( {{{180}^o} - {{175}^o}} \right) = \sin {5^o}\)
\(\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} - \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
Ta có: \(\sin {75^o} = \cos\left( {{{90}^o} - {{75}^o}} \right) = \cos {15^o}\); \(\sin {55^o} = \cos\left( {{{90}^o} - {{55}^o}} \right) = \cos {35^o}\)
\(\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} - \cos {15^o} - \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
Ta có: \(\tan {115^o} = - \tan \left( {{{180}^o} - {{115}^o}} \right) = - \tan {65^o}\)
Mà: \(\tan {65^o} = \cot \left( {{{90}^o} - {{65}^o}} \right) = \cot {25^o}\)
\(\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.(-\cot {25^o})\\ \Leftrightarrow D =- \tan {45^o} = -1\end{array}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Ta có: \(\cot {100^o} = - \cot \left( {{{180}^o} - {{100}^o}} \right) = - \cot {80^o}\)
Mà: \(\cot {80^o} = \tan \left( {{{90}^o} - {{80}^o}} \right) = \tan {10^o}\Rightarrow \cot {100^o} =- \tan {10^o}\)
\(\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.(-\tan {10^o})\\ \Leftrightarrow E = -\cot {30^o} =- \sqrt 3 .\end{array}\)
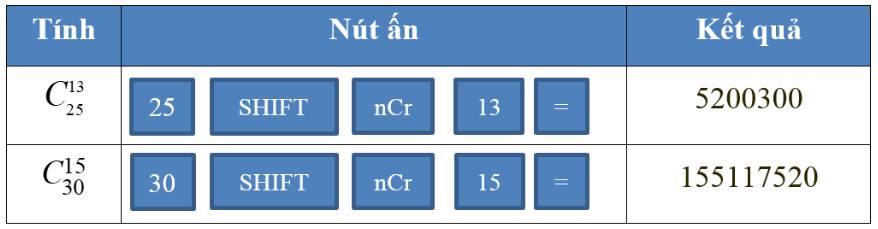
a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)
b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím
Thì ta nhận được kết quả là 495
c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím
Thì ta được kết quả là 1150