K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QD
19 tháng 4 2017
Lần lượt tính giá trị biểu thức tại x = 3, y = 4, z = 5; ta được
N: x2 = 32 = 9;
T: y2 = 42 =16;
Ă: 1212(xy + z) = 1212(3.4 +5)= 8,5;
L: x2 - y2 = 32 – 42 = -7;
M: t2 = x2 + y2 = 32 + 42 =25 → t = 5 (t là độ dài cạnh huyền);
Ê: 2x2 +1 = 2,52 + 1 = 51;
H: x2 + y2= 32 + 42 =25;
V: z2 – 1= 52 – 1 = 24;
I: 2(y + z) = 2(4 +5) =18;
Điền vào ô trống
Thông cảm mk bị cận!
18 tháng 4 2017
Hướng dẫn giải:
Trước hết ta thu gọn các đơn thức đồng dạng để xác định mỗi chữ cái tương ứng với kết quả nào trong ô trống của bảng.
V 2x2 + 3x2 – 1212 x2 = 9292 x2;
Ư 5xy – 1313 xy + xy = 173173 xy;
N - 1212 x2 + x2 = 1212 x2;
U - 6x2y – 6x2y = -12x2y ;
H xy – 3xy + 5xy = 3xy;
Ê 3xy2 – (-3xy2) = 6 xy2;
Ă 7y2z3 + (-7y2z3) = 0;
L - 1515 x2 + (- 1515 x2) = - 2525 x2;
Vậy tên của tác giả cuốn Đại VIệt sử kí là Lê Văn Hưu.
QD
20 tháng 4 2017
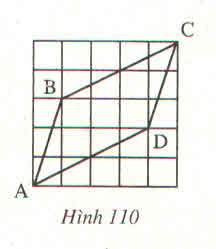
∆AHB và ∆ CKD có:
HB=KD.
AHB^=CKD^
AH=Ck
Nên ∆ AHB = ∆ CKD(c.g.c)
suy ra AB=CD.
tương tự ∆ CEB = ∆ AFD(c.g.c)
suy ra BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(câu a)
BC=AD(câu a)
BD chung.
Do đó ∆ABD=∆CDB(c.c .c)
Suy ra ˆABD=CDB^
Vậy AB // CD( hai góc so le trong bằng nhau)
SG
1
23 tháng 4 2017
Giải:
Do \(\left(2016a+13b-1\right)\left(2016^a+2016a+b\right)\) \(=2015\)
Nên \(2016a+13b-1\) và \(2016^a+2016a+b\) là 2 số lẻ \((*)\)
Ta xét 2 trường hợp:
Trường hợp 1: Nếu \(a\ne0\) thì \(2016^a+2016a\) là số chẵn
Do \(2016^a+2016a+b\) lẻ \(\Rightarrow b\) lẻ
Với \(b\) lẻ \(\Rightarrow13b-1\) chẵn do đó \(2016a+13b-1\) chẵn (trái với \((*)\))
Trường hợp 2: Nếu \(a=0\) thì:
\(\left(2016.0+13b-1\right)\left(2016^0+2016.0+b\right)\) \(=2015\)
\(\Leftrightarrow\left(13b-1\right)\left(b+1\right)=2015=1.5.13.31\)
Do \(b\in N\Rightarrow\left(13b-1\right)\left(b+1\right)=5.403=13.155\) \(=31.65\)
Và \(13b-1>b+1\)
\(*)\) Nếu \(b+1=5\Rightarrow b=4\Rightarrow13b-1=51\) (loại)
\(*)\) Nếu \(b+1=13\Rightarrow b=12\Rightarrow13b-1=155\) (chọn)
\(*)\) Nếu \(b+1=31\Rightarrow b=30\Rightarrow13b-1=389\) (loại)
Vậy \(\left(a,b\right)=\left(0;12\right)\)
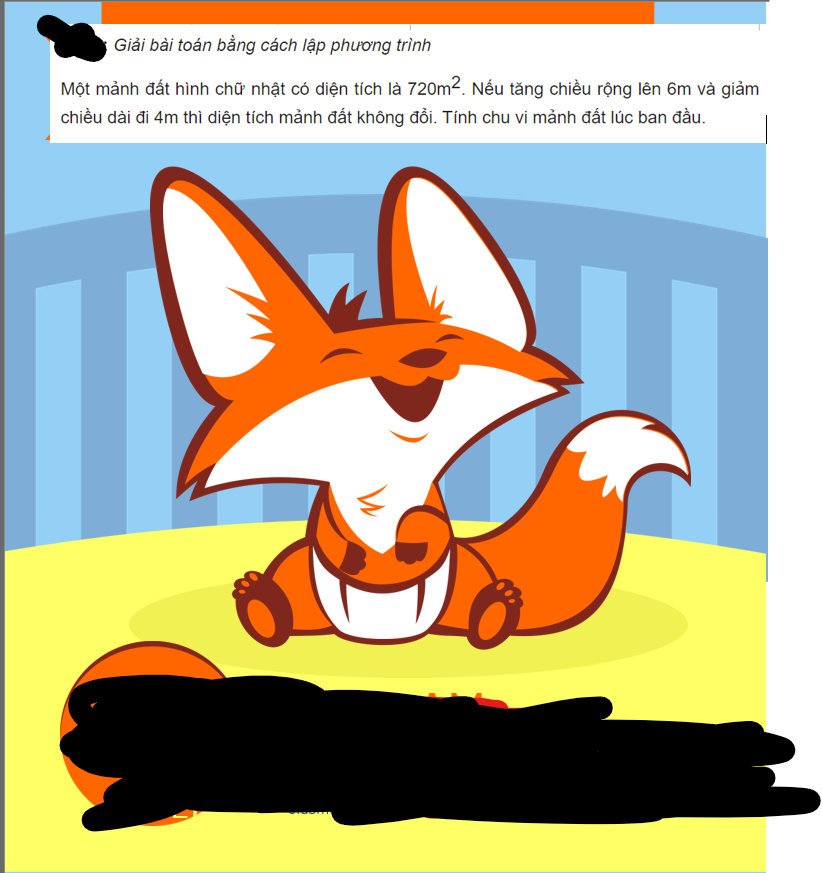
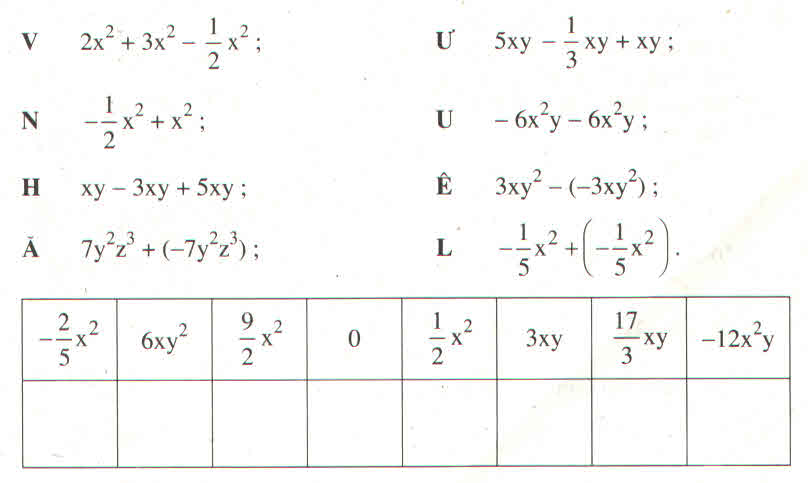
Gọi chiều rộng của mảnh đất hình chữ nhật là \(x\left(m,x>0\right)\)
Chiều dài của mảnh đất hình chữ nhật: \(\dfrac{720}{x}\left(m\right)\)
Chiều rộng mới của mảnh đất hình chữu nhật \(x+6\left(m\right)\)
Chiều dài mới của mảnh đất hình chữ nhật \(\dfrac{720}{x}-4\left(m\right)\)
Theo đề bài, ta có PT: \(\left(x+6\right)\left(\dfrac{720}{x}-4\right)=720\)
\(\Leftrightarrow720-4x+\dfrac{4320}{x}-24=720\)
\(\Leftrightarrow720x-4x^2+4320-24x-720x=0\)
\(\Leftrightarrow-4x^2-24x+4320=0\)
\(\Leftrightarrow\left(x-30\right)\left(x+36\right)=0\)
Vậy \(x=30\) (thoả mãn)
Chiều rộng của mảnh vườn hình chữ nhật 24m, chiều dài của mảnh vườn hình chữ nhật 30m
Chu vi của mảnh đất hình chữ nhật: \(\left(24+30\right).2=108m\)