Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lần lượt tính giá trị của biểu thức tại x = 3, y = 4, z = 5; ta được:

Vậy giải thưởng toán học Việt Nam mang tên nhà toán học nổi tiếng LÊ VĂN THIÊM.

Hướng dẫn giải:
Trước hết ta thu gọn các đơn thức đồng dạng để xác định mỗi chữ cái tương ứng với kết quả nào trong ô trống của bảng.
V 2x2 + 3x2 – 1212 x2 = 9292 x2;
Ư 5xy – 1313 xy + xy = 173173 xy;
N - 1212 x2 + x2 = 1212 x2;
U - 6x2y – 6x2y = -12x2y ;
H xy – 3xy + 5xy = 3xy;
Ê 3xy2 – (-3xy2) = 6 xy2;
Ă 7y2z3 + (-7y2z3) = 0;
L - 1515 x2 + (- 1515 x2) = - 2525 x2;

Vậy tên của tác giả cuốn Đại VIệt sử kí là Lê Văn Hưu.

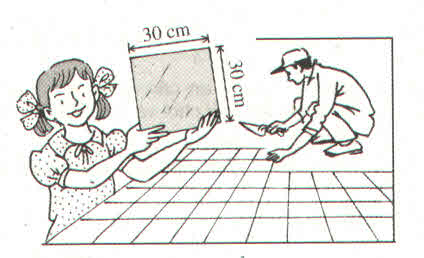
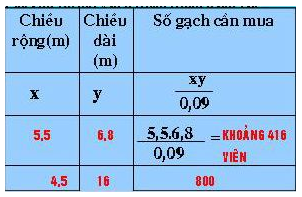
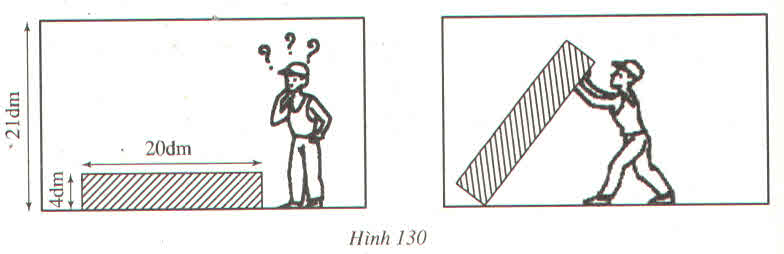
Gọi d là đường chéo của tủ. h là chiều cao của nhà. h= 21dm.
Ta có d2=202+42=400+16=416.
suy ra d= √416 (1)
Và h2=212=441, suy ra h= √441 (2)
So sánh (1) và (2) ta được d<h.
Như vậy anh Nam đẩy tủ đứng thẳng không bị vướng vào trần nhà.

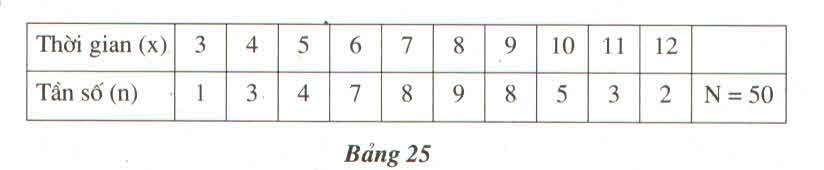
Căn cứ vào tháng sinh của các bạn trong lớp của mình để tìm tần số tương ứng. Sau đó điền kết quả vào bảng. Chẳng hạn điều tra tháng, năm sinh của một lớp tại một trường trung học cơ sở, ta có bảng thống kê số liệu ban đầu như sau:
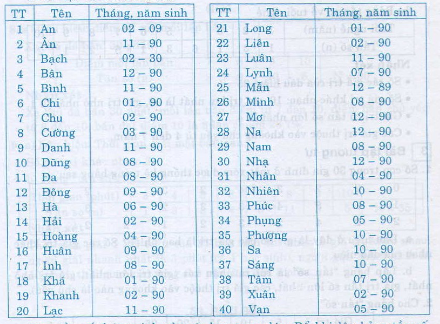
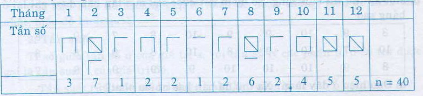
Tìm tần số tháng sinh của các bạn trong lớp. Để khi lập bảng tần số không nhần lẫn, ta kê ra tất cả các giá trị khác nhau của dấu hiệu (các tháng từ 1 - 12) lần lượt đọc tháng sinh từ trên xuống. Mỗi lần gặp tháng nào ta gạch vào cột tháng đó một vạch. Sau khi vạch xong, ta đếm số vạch của mỗi cột để ghi thành bảng "tần số" như sau:

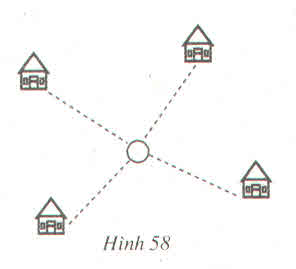
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.
Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: OA + OB + OC + OD
Ta có:
Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư là ngắn nhất.
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.
Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: OA + OB + OC + OD
Ta có:

Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư là ngắn nhất.




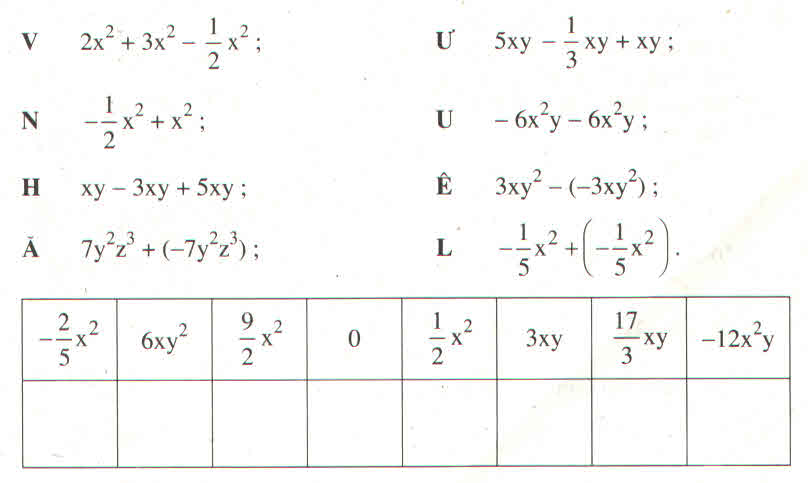








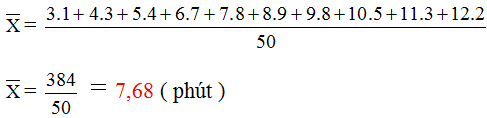
Lần lượt tính giá trị biểu thức tại x = 3, y = 4, z = 5; ta được
N: x2 = 32 = 9;
T: y2 = 42 =16;
Ă: 1212(xy + z) = 1212(3.4 +5)= 8,5;
L: x2 - y2 = 32 – 42 = -7;
M: t2 = x2 + y2 = 32 + 42 =25 → t = 5 (t là độ dài cạnh huyền);
Ê: 2x2 +1 = 2,52 + 1 = 51;
H: x2 + y2= 32 + 42 =25;
V: z2 – 1= 52 – 1 = 24;
I: 2(y + z) = 2(4 +5) =18;
Điền vào ô trống