Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

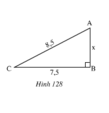
Áp dụng định lí Py–ta–go vào tam giác vuông ABC vuông tại B ta có:
AB2 + BC2 = AC2
Nên AB2 = AC2 – BC2
= 8,52 – 7,52
= 72,25 – 56,25
=16
⇒ AB = 4 (m)

Tam giác ABC vuông ở B,áp dụng định lí py‐ta‐go với tam giác này ta có:
AC 2=AB 2+BC 2
suy ra: AB 2=AC 2 ‐BC 2=8,5 2 ‐7,5 2=72,25‐56,25=16
=>AB 2=16;AB=4
Vậy chiều dài AB=4cm
TAM GIÁC ABC VUÔN TẠI B ,AD ĐL PYTAGO TA CÓ
ACC^2=AB^2+BC^2=>AB^2=AC^2-BC^2
=>AB^2=16
=>AB=4(M)

#Tự vẽ hình nhé bạn#k mình nha#Thanks#
a ) Xét \(\Delta\)ABC và \(\Delta\)DMC có :
- AC = CD ( giả thiết )
- BC = CM ( giả thiết )
- Góc BCA = Góc MCD ( đối đỉnh )
\(\Rightarrow\)\(\Delta\)ABC = \(\Delta\)DMC ( c - g - c )
b ) Ta có : \(\Delta\)ABC = \(\Delta\)DMC ( chứng minh trên )
\(\Rightarrow\)\(BÂC\) = Góc MDC ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong nên\(AB // MD\)
c ) Xét \(\Delta\)IAC và \(\Delta\) NDCcó :
- Góc ICA = Góc NCD ( đối đỉnh )
- AC = CD ( giả thiết )
- BÂC = Góc CDN ( chứng minh trên )
\(\Rightarrow\)\(\Delta\)IAC = \(\Delta\)NDC ( g - c - g )
\(\Rightarrow\)IA = ND ( 2 cạnh tương ứng )
Ta có : IB + AI = AB nên IB = AB - AI
Ta lại có : MN + ND = MD nên MN = MD - ND
Mà AB = MD và AI = ND
\(\Rightarrow\)IB = MN

Gọi: AB là độ cao con đê
BC là đoạn lên dốc của con đê
AC là khoảng cách từ chân dốc đến chân đê
Xét tg ABC vuông tại A, có:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=>AC^2=BC^2-AB^2\)
\(=>AC=\sqrt{BC^2-AB^2}=\sqrt{8,5^2-4^2}=7,5\left(m\right)\)
Vậy............

chiều cao AB là
\(\sqrt{8,5^2-7,5^2}=\sqrt{72,25-56,25}=\sqrt{16}=4\)
vậy chiều cao AB là 4m

mk nghĩ từ sáng đến giờ
Tự giải
Bài giải
Gọi thời gian đi từ A->B là (t1)
Thời gian đi từ B->A là (t2)
Ta có (Đây là t1;t2nha mk viết dưới công thức nên nó giống phân số)
\(12_{ }t_1+6\left(\frac{5}{4}-t_1\right)=8t_2+4\left(\frac{3}{2}-t_2\right)\left(1\right)\)
và \(t_2-t_1=\frac{3}{2}-\frac{5}{4}=\frac{1}{2}\)
Ta có
12t1\(+\frac{30}{4}-6t_1=8t_2+6-4t_2\)
\(\Leftrightarrow4t_2-6t_1=\frac{3}{2}\)
Vậy giải hệ phương trình
\(\hept{\begin{cases}4t_2-6t_1=\frac{3}{2}\\t_2-t_1=\frac{1}{2}\end{cases}}\)Ta đc
\(\hept{\begin{cases}t_1=\frac{1}{4}\\t_{2=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}}\end{cases}}\)
Vậy SAB=12.\(\frac{1}{4}\)+b(\(\frac{5}{4}-\frac{1}{4}\))
SAB=3+6=9 (km)
Vậy quãng đường AB dài 9km
hc tốt ~~~
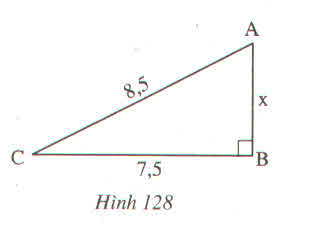
Tam giác ABC vuông ở B,áp dụng định lí py-ta-go với tam giác này ta có:
AC2=AB2+BC2 suy ra:
AB2=AC2-BC2=8,52-7,52=72,25-56,25=16
=>AB2=16;AB=4
Vậy chiều dài AB=4cm
A B C 8,5cm 7,5cm