Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

∆AHB và ∆ CKD có:
HB=KD.
AHB^=CKD^
AH=Ck
Nên ∆ AHB = ∆ CKD(c.g.c)
suy ra AB=CD.
tương tự ∆ CEB = ∆ AFD(c.g.c)
suy ra BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(câu a)
BC=AD(câu a)
BD chung.
Do đó ∆ABD=∆CDB(c.c .c)
Suy ra ˆABD=CDB^
Vậy AB // CD( hai góc so le trong bằng nhau)

Xét ∆AHB và ∆ CKD có:
HB=KD.
ˆAHB=ˆCKD
AH=CK
=> ∆ AHB = ∆ CKD(c.g.c)
=> AB=CD.( 2 canh tương ứng)
tương tự ∆ CEB = ∆ AFD(c.g.c)
=> BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(CMT)
BC=AD(CMT)
BD chung.
=> ∆ABD=∆CDB(c.c .c)
=> ˆABD^=ˆCDB( 2 góc tương ứng)
=> AB // CD( hai góc so le trong bằng nhau)

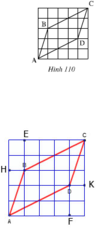
+ ΔAHB và ΔCKD có
HB = KD (=1)
góc AHB = góc CKD(=90º)
AH = CK (=3).
⇒ ΔAHB = ΔCKD(c.g.c)
⇒AB = CD (hai cạnh tương ứng)
+ ΔCEB và ΔAFD có
BE = DF (=2)
góc BEC = góc DFA (=90º)
CE = AF (=4).
⇒ ΔCEB = ΔAFD ( c.g.c)
⇒ BC = AD (hai cạnh tương ứng)

ΔABD và ΔCDB có
AB = CD
AD = BC
BD cạnh chung
⇒ ΔABD = ΔCDB (c.c.c)
⇒ góc ABD = góc CDB (hai góc tương ứng)
Vậy AB // CD ( hai gó so le trong bằng nhau )

a, xét 2 tam giác vuông AEC và AED có:
AC=AD(gt)
AE cạnh chung
=> t.giác AEC=t.giác AED(cạnh huyền-cạnh góc vuông)
=> \(\widehat{CAE}\)=\(\widehat{DAE}\)=> AE là p/g của \(\widehat{CAD}\)<=> AE là p/g của \(\widehat{CAB}\)
b, xét t.giác AIC và t.giác AID có:
AI cạnh chung
\(\widehat{IAC}\)=\(\widehat{IAD}\)(theo câu a)
AC=AD(gt)
=> t.giác AIC=t.giác AID(c.g.c)
=> IC=ID=> I là trung điểm của CD(1)
\(\widehat{AIC}\)=\(\widehat{AID}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AIC}\)=\(\widehat{AID}\)=90 độ=> AI\(\perp\)CD(2)
từ (1) và (2) suy ra AE là trung trực của CD
A B C D E I

a) Xét tam giac AMB và tam giac AMC
có AB=AC
AM chung
BM=CM
suy ra tam giac BMA= tam giac CMA
b) Xét tam giac DAM va tam giac CMA
co AM chung
góc DAM= goc CMA( do DA//MC
AMD=CAM
=) TAM GIAC DAM= TAM GIAC CMA
=)DA= CM