Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E K F a) Hình thang ABCD có:
E là trung điểm của AD (1)
F là trung điểm của BC
=> EF là đường trung bình của hình thang ABCD
nên EF// CD
=> EK // CD (2)
Từ (1)(2) => KA = KC
b) * Xét tam giác ACD có:
EA =ED (gt)
KA = KC (cmt)
=> EK là đường trung bình của tam giác ACD
=>EK = 1/2 CD
=>CD = 6 x 2
CD= 12 cm
* Tương tự chứng minh KF là đường trung bình của tam giác ABC
=> KF =1/2 AB
=>AB = 2 x 2
AB = 4 cm

Xét hình thang ABCD có:
AE = DE
BF = CF
=> EF là đường trung bình của hình thang ABCD
=> EF// AB và DC (1)
Mà : K ∈ EF (2)
Từ (1), (2) => EK // DC
Xét tam giác ADC có
AE = DE
EK// DC
=> AK = CK
b, Xét tam giác ADC có
AE = DE
AK =CK
=> EK là đường trung bình của tam giác ADC
=> EK = \(\frac{1}{2}\)DC
Mà: DC = 10 cm
=> EK = 5cm
Ta có: Tam giác ABC có:
BF = CF
AK = CK
=> KF là đường trung bình của tam giác ABC
=> KF = \(\frac{1}{2}\)AB
Mà: AB = 4cm
=> KF = 2 cm
Vậy EK = 5cm
KF = 2cm
Cậu xem lại nhé.
a) Xét hình thang ABCD có :
E là trung điểm của AD
F là trung điểm của BC
Nên : EF là đường trung bình của hình thang ABCD
Do đó : EF // AB // CD và EF = \(\frac{AB+CD}{2}\)
Xét △ ABC có :
F là trung điểm của BC
KF // AB ( K ∈ EF, EF // AB )
Nên : KF là đường trung bình của △ ABC
D o đó : K là trung điểm của AC
b) Theo câu a) ta có : KF là đương trung bình của △ ABC
Nên : KF = \(\frac{AB}{2}\) = 4 : 2 = 2 ( cm )
Lại có : EF = \(\frac{AB+CD}{2}\)
Do đó : EF = \(\frac{4+10}{2}\)= 7 ( cm )
Mà : EK = EF - KF
Suy ra : EK = 7 - 2 = 5 ( cm )

bài 1
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2= (AB +CD)/2
Vậy EF ≤ (AB +CD)/2

.png)
a) Xét tam giác ABD có E và K lần lượt là trung điểm của AD và DB nên EK là đường trung bình tam giác ABD.
Vậy thì EK // AB
Hoàn toàn tương tự ta có ngay KF // DC, hay KF // AB.
Ta thấy, từ một điểm K có hai đoạn thẳng EK và KF cùng song song với AB. Theo tiên đề Oclit ta có E, K, F thẳng hàng.
b) Xét tam giác ABC có F là trung điểm BC, IF // AB nên IF là đường trung bình tam giác ABC.
Vậy thì AI = IC.
c) Xét tam giác ADC có E, I lần lượt là trung điểm của AD và AC nên EI là đường trung bình tam giác ADC.
Vậy thì \(EI=\frac{DC}{2}\)
Tương tự \(KF=\frac{DC}{2}\)
Vậy nên EI = KF.
Từ đó ta có: EI - KI = KF - KI hay EK = IF.
d) Ta có KF = DC/2 = 10 : 2 = 5 (cm)
IF = AB/2 = 6 : 2 = 3 (cm)
Vậy thì KI = KF - IF = 2 (cm)

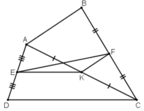
a) + ΔADC có: AE = ED (gt) và AK = KC (gt)
⇒ EK là đường trung bình của ΔADC
⇒ EK = CD/2
+ ΔABC có AK = KC (gt) và BF = FC (gt)
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB/2.
b) Ta có: EF ≤ EK + KF = 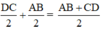
(Bổ sung: 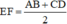 ⇔ EF = EK + KF ⇔ E, F, K thẳng hàng ⇔ AB // CD)
⇔ EF = EK + KF ⇔ E, F, K thẳng hàng ⇔ AB // CD)
