
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


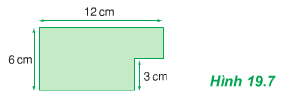
Chia bản mỏng thành hai phần.
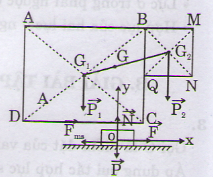
ABCD và BMNQ. Trọng tâm của 2 phần này là G1 và G2. Nếu gọi trọng tâm của bản lề G thì G sẽ là điểm đặt của hợp lực của các trọng lực P1 và P2 của hai bản nói trên.
Do trọng lượng của mỗi tấm tỉ lệ với diện tích.
Ta có: =
=
= 6
Khi đó G được xác định như sau:
=
= 6 (1)
Mặt khác ta có: G1G2 = = 6,18 cm
=> GG1 + GG2 = 6,18 (2)
(1)và(2) => GG1 = 0,882 cm
Vậy trọng tâm G nằm trên đường nối G1 và G2; cách G1 một đoạn 0,882cm

Chọn B.
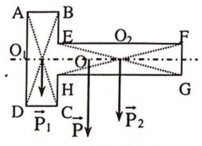
Ta chia bản mỏng ra thành hai phần ABCD và EFGH, mỗi phần có dạng hình chữ nhật. Trọng tâm của các phần này nằm tại O 1 , O 2 (giao điểm các đường chéo của hình chữ nhật). Gọi trọng tâm của bản là O, O sẽ là điểm đặt của hợp các trọng lực P ⇀ 1 , P 2 ⇀ của hai phần hình chữ nhật.
Theo qui tắc hợp lực song song cùng chiều:
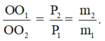
Vì bản đồng chất nên khối lượng tỉ lệ với diện tích :
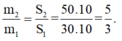
Đồng thời: O 1 O 2 = O O 1 + O O 2 = 60/2 = 30cm.
Từ các phương trình trên, ta suy ra:
O O 1 = 18,75cm; O O 2 = 11,25cm.
Vậy trọng tâm O nằm trên trục đối xứng, cách đáy: 11,25 + 25 = 36,25cm.

Chọn B.
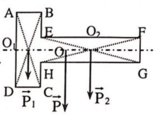
Ta chia bản mỏng ra thành hai phần ABCD và EFGH, mỗi phần có dạng hình chữ nhật. Trọng tâm của các phần này nằm tại O1, O2 (giao điểm các đường chéo của hình chữ nhật). Gọi trọng tâm của bản là O, O sẽ là điểm đặt của hợp các trọng lực P 1 → , P 2 → của hai phần hình chữ nhật.
Theo qui tắc hợp lực song song cùng chiều:
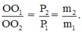
Vì bản đồng chất nên khối lượng tỉ lệ với diện tích :
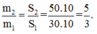
Đồng thời: O1O2 = OO1 + OO2 = 60/2 = 30cm.
Từ các phương trình trên, ta suy ra: OO1 = 18,75cm; OO2 = 11,25cm.
Vậy trọng tâm O nằm trên trục đối xứng, cách đáy: 11,25 + 25 = 36,25cm.

Đáp án B
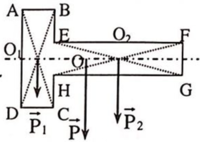
Ta chia bản mỏng ra thành hai phần ABCD và EFGH, mỗi phần có dạng hình chữ nhật. Trọng tâm của các phần này nằm tại O1, O2 (giao điểm các đường chéo của hình chữ nhật). Gọi trọng tâm của bản là O, O sẽ là điểm đặt của hợp các trọng lực ![]() của hai phần hình chữ nhật.
của hai phần hình chữ nhật.



Áp dụng phương pháp tọa độ :
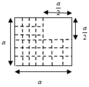
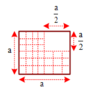
x G = y G = m a 4 + m a 4 + m 3 a 4 3 m = 5 a 12

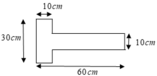
Cách 1 : Ta chia bản mỏng ra thành hai phần. Trọng tâm của các phần này nằm tai O1, O2 như hình vẽ
Gọi trọng tâm của bản là O, là điểm đặt của hợp các trọng lực P → 1 , P → 2 của hai phần hình chữ nhật.
Theo quy tắc hợp lực song song cùng chiều
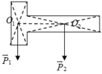
O O 1 O O 2 = P 2 P 1 = m 2 m 1
Bản đồng chất, khối lượng tỉ lệ với diện tích
m 2 m 1 = S 2 S 1 = 50.10 30.10 = 5 3
Ngoài ra:
O 1 O 2 = O O 1 + O O 2 = 60 2 = 30 c m
Từ các phương trình trên
⇒ O O 1 = 18 , 75 c m ; O O 2 = 11 , 25 c m
Cách 2 : Xác định O theo công thức tọa độ trọng tâm
Trọng tâm O của bản nằm trên trục đối xứng Ix.

Tọa độ trọng tâm O
x = I O = m 1 x 1 + m 2 x 2 m 1 + m 2
Trong đó:
{ x 1 = I O 1 = 55 c m x 2 = I O 2 = 25 c m m 2 m 1 = S 2 S 1 = 5 3 h a y m 2 = 5 3 m 1
⇒ x = I O = m 1 .55 + 5 3 . m 1 .25 m 1 + 5 3 . m 1 = 36 , 25 c m
Trọng tâm O của bản ở cách I: 36,25cm

Chọn đáp án A
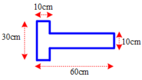
Ta chia bản mỏng ra thành hai phần. Trọng tâm của các phân này nằm tại O 1 , O 2 như hình vẽ
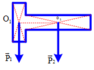
Gọi trọng tâm của bản là O, là điểm đặt của hợp các trọng lực của hai phần hình chữ nhật.
Theo quy tắc hợp lực song song cùng chiều O O 1 O O 2 = P 2 P 1 = m 2 m 1
Bản đồng chất khối lượng tỉ lệ với diện tích m 2 m 1 = S 2 S 1 = 50.10 30.10 = 5 3
Ngoài ra O O 1 = O O 1 + O O 2 = 60 2 = 30 c m
Từ các phương trình: O O 1 = 18 , 75 c m ; O O 2 = 11 , 25 c m

Chọn đáp án D
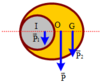
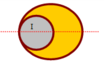
Do tính đối xúng → G nằm trên đường thẳng OO' về phía đầy
Trọng tâm của đĩa nguyên vẹn là tâm O; trọng tâm của đĩa bị khoét là O'

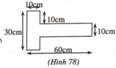
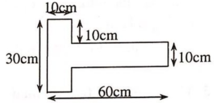
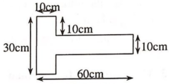
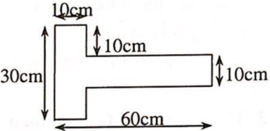

Ta chia bản mỏng ra thành hai phần ABCD và EFGH, mỗi phần có dạng hình chữ nhật. Trọng tâm của các phần này nằm tại O1, O2 (giao điểm các đường chéo của hình chữ nhật). Gọi trọng tâm của bản là O, O sẽ là điểm đặt của hợp các trọng lực của hai phần hình chữ nhật. (hình 84)
Theo qui tắc hợp lực song song cùng chiều: