Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thay x=-3 vào phương trình 2x2 – m2x +18m =0 ta được:
2(-3)2 - m2(-3) + 18m =0 ⇔ 3m2 +18m+18 =0
⇔ m2 + 6m +6 = 0
Δ' = 32 -1.6 = 9 -6 =3 > 0
√Δ' = √3
Phương trình có 2 nghiệm phân biệt:
Vậy với m=3 - 3 hoặc m=- 3- 3 thì phương trình đã cho có nghiệm x= -3
b) Thay x = -2 vào phương trình mx2 – x – 5m2 = 0 ta được:
m(-2)2 – (-2) – 5m2=0 ⇔ 5m2 – 4m -2 =0
Δ' = (-2)2 -5.(-2) = 4+10 = 14 > 0
√Δ' = √14
Phương trình có 2 nghiệm phân biệt:

(Bạn viết phương trình nhé, nó dài nên ngại viết lắm =.=) (a = 1; b' = - m - 1; c = m ^ 2)
Xét phương trình trên có a = 1 khác 0 => Phương tình là phương trình bậc 2 một ẩn
Để phương trình có 2 nghiệm phân biệt <=> \(\Delta'>0\)
<=> b' ^ 2 - ac > 0
<=> (- m - 1) ^ 2 - 1. m ^ 2 > 0
<=> m ^2 + 2m + 1 - m ^ 2 > 0
<=> 2m + 1 > 0
<=> 2m > - 1
<=> m > - 0,5
Vậy để phương trrình có 2 nghiệm phân biệt thì m > - 0,5

a) x2 – 2(m – 1)x + m2 = 0 có a = 1, b = -2(m - 1), b' = -(m - 1), c = m2
∆' = [-(m - 1)]2 – m2 = m2 – 2m + 1 – m2 = 1 – 2m
b) Ta có ∆’ = 1 – 2m
Phương trình có hai nghiệm phân biệt khi 1 – 2m > 0 hay khi m < \(\dfrac{1}{2}\)
Phương trình vô nghiệm khi m > \(\dfrac{1}{2}\)
Phương trình có nghiệm kép khi m = \(\dfrac{1}{2}\).
a) x2 – 2(m – 1)x + m2 = 0 có a = 1, b = -2(m - 1), b' = -(m - 1), c = m2
∆' = [-(m - 1)]2 – m2 = m2 – 2m + 1 – m2 = 1 – 2m
b) Ta có ∆’ = 1 – 2m
Phương trình có hai nghiệm phân biệt khi 1 – 2m > 0 hay khi m <
Phương trình vô nghiệm khi m >
Phương trình có nghiệm kép khi m = .

a) Tam thức bậc hai có \(\Delta'=m^2-m+4=m^2-2.\frac{1}{2}m+\frac{1}{4}-\frac{1}{4}+4=\left(m-\frac{1}{2}\right)^2+\frac{15}{4}>0\).
Suy ra phương trình (1) luôn có nghiệm với mọi m.
b) Theo Vi-et ta có:
\(x_1+x_2=2m,x_1.x_2=m-4\)
Điều kiển để \(x_1+x_2=\frac{x_1^2}{x_2}+\frac{x_2^2}{x_1}\)
\(\Leftrightarrow x_1+x_2=\frac{x_1^3+x_2^3}{x_1x_2}\)
\(\Leftrightarrow x_1+x_2=\frac{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)}{x_1x_2}\)
\(\Leftrightarrow2m=\frac{\left(2m\right)^3-3\left(m-4\right).2m}{m-4}\)
\(\Leftrightarrow2m\left(m-4\right)=8m^3-6m^2+8m\) và \(m\ne4\)
\(\Leftrightarrow4m\left(2m^2-2m+3\right)=0\) và \(m\ne4\)
\(\Leftrightarrow m=0\)

ta có phương trình x^2 +3x +m =0
nên để pt có 2 nghiệm phân biệt thì 9 - 4m > 0 hay m <9/4
theo Viét nếu x1 và x2 là 2 nghiệm của pt thì
x1 +x2 =-3 (1)và
x1*x2=m => 2x1*x2 =2m (2)
=> x1^2 +x2^2 +2m = (x1 +x2 )^2 (từ (1) và (2) )( cái hằng đẳng thức chắc bạn phải biết r đúng ko )
mà x1 +x2 =-3 ,,,x1^2 +x2^2 = 31 nên ta có
31 +2m =9
m = -11

Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
\(x^2_1+x^2_2=\left(x_1+x_2\right)^2-2x_1x_2\\ =\left[\dfrac{-2\left(m-1\right)^2}{7}\right]-2\dfrac{\left(-m\right)^2}{7}\\ =\dfrac{4m^2-8m+4}{49}+\dfrac{2m^2}{7}\\ =\dfrac{4m^2-8m+4+14m^2}{49}\\ =\dfrac{18m^2-8m+4}{49}\)
Vậy \(x^2_1+x^2_2=\dfrac{18m^2-8m+4}{49}\).
Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
x\(\dfrac{1}{2}\)+x\(\dfrac{2}{2}\)=(x1+x2)2−2x1x2
=[\(\dfrac{-2\left(m-1\right)^2}{7}\)]-2\(\dfrac{\left(-m\right)^2}{7}\)
=\(\dfrac{4m^2-8m+4}{49}\)+\(\dfrac{2m^2}{7}\)
=\(\dfrac{4m^2-8m+4+14m^2}{49}\)
=\(\dfrac{18m^2-8m+4}{49}\)
vậy x\(\dfrac{2}{1}\)+x\(\dfrac{2}{2}\)=\(\dfrac{18m^2-8m+4}{49}\)
![]()
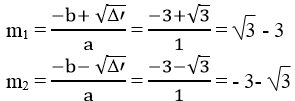

Thay x = -2 vào phương trình m x 2 – x – 5 m 2 = 0 ta được:
m - 2 2 – (-2) – 5 m 2 = 0
⇔ - 5 m 2 + 4m + 2 = 0
⇔ 5 m 2 – 4m - 2 = 0 (Có a = 5; b = -4 nên b’ = - 2; c = - 2)
∆ ' = - 2 2 -5.(-2) = 4 + 10 = 14 > 0
∆ ' = 14