

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)

Đáp án C
Vân sáng bậc 3 cách vân trung tâm 2,4mm => Khoảng vân
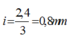
Nên áp dụng công thức tính khoảng vân ta có:
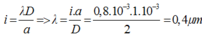

Phương pháp: Sử dụng công thức tính khoảng vân và công thức xác định vị trí vân sáng, tối
Cách giải:
Vân sáng bậc 3 cách vân trung tâm 2,4mm => Khoảng vân i = 2,4/3 = 0,8 mm
Nên áp dụng công thức tính khoảng vân ta có:
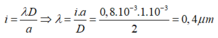
Đáp án C

Chọn C
vân sáng bậc 3 cách vân trung tâm 2,4 mm tức là: x0+3 - x0 = 2,4 mm <=> 3i = 2,4 => i = 0,8mm
Bước sóng của ánh sáng đơn sắc dùng trong thí nghiệm là:
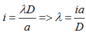
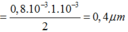

Đáp án A
+ Khoảng cách giữa vân sáng bậc hai đến vân sáng bậc năm là
Δ x = 3 i = 3 D λ a = 3 1 , 5.0 , 6.10 − 6 0 , 2.10 − 3 = 13 , 5 mm

Vân sáng bậc 4 cách vân trung tâm là
\(x_ 4 = 4.i = 4.\frac{\lambda D}{a} = 3,2mm.\)
Chú ý nếu giữ nguyênđơn vị của \(\lambda (\mu m)\), D(m), a(mm) thì khi đó kết quả cho \(x\) ra đơn vị là mm.

Tóm tắt:
a = \(10^{-3}m\)
D = \(1,25m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=k_2\lambda_2\Rightarrow\)\(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,48}{0,64}=\frac{3}{4}\)
Vậy: \(k_1=3;k_2=4\)\(\Rightarrow\Delta x=3i_1=3.\frac{\lambda_1.D}{a}=3.\)\(\frac{0,64.10^{-6}.1,25}{10^{-3}}=2,4.10^{-3}m=2,4mm\)
\(\rightarrow D\)