Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi A a ; 0 ; 0 , B ( 0 ; b ; 0 ) , C 0 ; 0 ; c → phương trình mặt phẳng (ABC) là x a + y b + z c = 1
Vì điểm M 1 ; 2 ; 3 ∈ P ⇒ 1 a + 2 b + 3 c = 1 , ta có 1 a + 2 b + 3 c 2 ≤ 1 2 + 2 2 + 3 2 1 a 2 + 1 b 2 + 1 c 2
Khi đó 1 O A 2 + 1 O B 2 + 1 O C 2 = 1 a 2 + 1 b 2 + 1 c 2 ≥ 1 14 . Dâu bằng xảy ra khi và chỉ khi a = 2b = 3c.
Suy ra a = 14 , b = 7 , c = 14 3 , vậy phương trình mặt phẳng (P) là x 14 + y 7 + 3 z 14 = 1 ⇔ x + 2 y + 3 z - 14 = 0 .

Đáp án D.
Xét tứ diện vuông OABC có OA, OB, OC đôi một vuông góc nên hình chiếu của O lên mặt phẳng (ABC) chính là trực tâm H của tam giác ABC và d O ; ( A B C ) = h
Ta có 1 h 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 , nên 1 O A 2 + 1 O B 2 + 1 O C 2 có giá trị nhỏ nhất khi d O ; A B C lớn nhất.
Mặt khác d O ; A B C ≤ O M , ∀ M ∈ P . Dấu "=" xảy ra khi H ≡ M hay mặt phẳng (P) đi qua M(1;2;3) và có vectơ pháp tuyến là O M → = ( 1 ; 2 ; 3 ) .
Vậy P : 1 x - 1 + 2 ( y - 2 ) + 3 z - 3 = 0 ⇔ x + 2 y + 3 z - 14 = 0

Chọn B
Xét tứ diện vuông OABC, gọi H là hình chiếu vuông góc của O lên (ABC). Dễ thấy H là trực tâm của tam giác ABC. Khi đó

có giá trị nhỏ nhất khi OH đạt giá trị lớn nhất.
Mặt khác OH≤OM và độ dài OM là không đổi. Do đó OH đạt giá trị lớn nhất bằng OM.
Điều này xảy ra khi H≡M Khi đó (P) là mặt phẳng qua M và có một vecto pháp tuyến là O M → = 1 ; 2 ; 3 nên phương trình mặt phẳng (P) là


Đáp án A.
6 x - 3 y + 2 z - 12 = 0 .
Tương tự
B 0 ; 4 ; 0 , C 0 ; 0 ; 6 ⇒ A B C : x 2 + y 4 + z 6 = 1 ⇔ 6 x + 3 y + 2 z − 12 = 0.

ta có \(y=\frac{3\left(x+1\right)}{x-2}=3+\frac{9}{x-2}\) để các điểm trên C có tọa độ nguyên thì (x,y) nguyên
suy ra (x-2) là ước của 9
mà \(Ư\left\{9\right\}=\left\{\pm9;\pm3;\pm1\right\}\)
TH1: x-2=-9 suy ra x=-7 suy ra y=3-1=2
th2: x-2=9 suy ra x=11 suy ra y=3+1=4
th3:x-2=-3 suy ra x=-2 suy ra y=3-3=0
th4: x-2=3 suy ra x=5 suy ra y=3+3=6
th5:x-2=1 suy ra x=3 suy ra y=3+9=12
th6: x-2=-1 suy ra x=1 suy ra y=3-9=-6
kết luận....



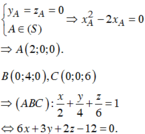

Chọn đáp án C.