Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Xét tứ diện vuông OABC có OA, OB, OC đôi một vuông góc nên hình chiếu của O lên mặt phẳng (ABC) chính là trực tâm H của tam giác ABC và d O ; ( A B C ) = h
Ta có 1 h 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 , nên 1 O A 2 + 1 O B 2 + 1 O C 2 có giá trị nhỏ nhất khi d O ; A B C lớn nhất.
Mặt khác d O ; A B C ≤ O M , ∀ M ∈ P . Dấu "=" xảy ra khi H ≡ M hay mặt phẳng (P) đi qua M(1;2;3) và có vectơ pháp tuyến là O M → = ( 1 ; 2 ; 3 ) .
Vậy P : 1 x - 1 + 2 ( y - 2 ) + 3 z - 3 = 0 ⇔ x + 2 y + 3 z - 14 = 0

Chọn B
Xét tứ diện vuông OABC, gọi H là hình chiếu vuông góc của O lên (ABC). Dễ thấy H là trực tâm của tam giác ABC. Khi đó

có giá trị nhỏ nhất khi OH đạt giá trị lớn nhất.
Mặt khác OH≤OM và độ dài OM là không đổi. Do đó OH đạt giá trị lớn nhất bằng OM.
Điều này xảy ra khi H≡M Khi đó (P) là mặt phẳng qua M và có một vecto pháp tuyến là O M → = 1 ; 2 ; 3 nên phương trình mặt phẳng (P) là


Đáp án A
Gọi pt mặt phẳng cần tìm là: x a + y b + z c = 1 M ( 1 ; 1 ; 2 ) ∈ ( P ) ⇒ 1 a + 1 b + 2 c = 1 ( * ) A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) : O A = O B = O C ⇒ a = b = c = α > 0 ⇒ ( a ; b ; c ) ∈ { ( α ; α ; α ) , ( − α ; α ; α ) , ( α ; − α ; α ) , ( α ; α ; − α ) , ( − α ; − α ; α ) , ( − α ; α ; − α ) , ( α ; − α ; − α ) , ( − α ; − α ; − α ) }
Thay vào (*) ta thấy chỉ có 3 bộ thỏa mãn: ( α ; α ; α ) , ( − α ; α ; α ) , ( α ; − α ; α ) tương ứng có 3 mặt phẳng thỏa mãn đề bài
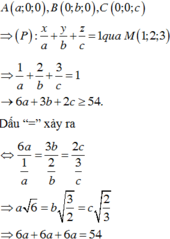
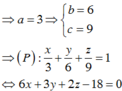







Đáp án A
Gọi A a ; 0 ; 0 , B ( 0 ; b ; 0 ) , C 0 ; 0 ; c → phương trình mặt phẳng (ABC) là x a + y b + z c = 1
Vì điểm M 1 ; 2 ; 3 ∈ P ⇒ 1 a + 2 b + 3 c = 1 , ta có 1 a + 2 b + 3 c 2 ≤ 1 2 + 2 2 + 3 2 1 a 2 + 1 b 2 + 1 c 2
Khi đó 1 O A 2 + 1 O B 2 + 1 O C 2 = 1 a 2 + 1 b 2 + 1 c 2 ≥ 1 14 . Dâu bằng xảy ra khi và chỉ khi a = 2b = 3c.
Suy ra a = 14 , b = 7 , c = 14 3 , vậy phương trình mặt phẳng (P) là x 14 + y 7 + 3 z 14 = 1 ⇔ x + 2 y + 3 z - 14 = 0 .