Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Gọi M x ; y ; z
⇒ A M → = x − 10 ; y − 6 ; z + 2 ; B M → = x − 5 ; y − 10 ; z + 9
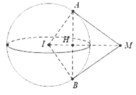
Gọi H, K lần lượt là hình chiếu của A, B lên
có A M H ^ = B M K ^ .
Khi đó sin A M H ^ = A H M A sin B M K ^ = B K M B
⇒ A H M A = B K M B ⇒ M A = 2 M B ⇔ M A 2 = 4 M B 2 .
Suy ra
x − 10 2 + y − 6 2 + z + 2 2 = 4 x − 5 2 + y − 10 2 + z + 9 2
⇔ x 2 + y 2 + z 2 − 20 3 x − 68 3 y + 68 3 z + 228 = 0 ⇔ S : x − 10 3 2 + y − 34 3 2 + z − 34 3 2 = R 2 .
Vậy M ∈ C là giao tuyến của α và S
→ Tâm I 2 ; 10 ; − 12 .

Chọn đáp án A
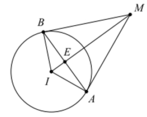
Mặt cầu (S) có tâm I(1;1;0) bán kính R = 2. Kẻ tiếp tuyến MA và MB sao cho M, A, I, B đồng phẳng suy ra đường tròn (C) là đường tròn đường kính AB.


Chọn A.
Phương pháp: Dùng hệ thức lượng trong tam giác vuông để tính.
Cách giải:


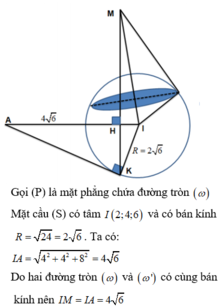





Gọi (P) là mặt phẳng chứa đường tròn ( ω )
Mặt cầu (S) có tâm I(2;4;6) và có bán kính R = 24 = 2 6 . Ta có:
I A = 4 2 + 2 2 + 8 2 = 4 6
Do hai đường tròn ω và ω ' có cùng bán kính nên IA=IM = 4 6
Tam giác IAK vuông tại K nên ta có
I K 2 = I H . I A ⇒ I H = I K 2 I A = 24 4 6 = 6
Do H là tâm của đường tròn ω nên điểm H cố định.
Tam giác IHM vuông tại H nên ta có:
M H = I M 2 - I H 2 = 4 6 2 - 6 2 = 3 10
Do H cố định thuộc mặt phẳng (P), M di động trên mặt phẳng (P) và M H = 3 10 không đổi. Suy ra điểm M thuộc đường tròn có tâm là H và có bán kính r = H M = 3 10
Chọn đáp án B.