
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



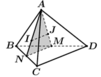
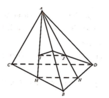
Gọi M, N lần lượt là trung điểm của BD, DC
Mà I, J lần lượt là trọng tâm các tam giác ABC, ABD nên:
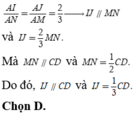

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án B
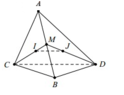
Gọi M là trung điểm của AB
Tam giác ABC có trọng tâm I suy ra M I M C = 1 3
Tam giác ABC có trọng tâm J suy ra M J M D = 1 3
Khi đó M I M C = M J M D ⇒ I J / / C D (định lí Talet)

a d e m n b c i h
a, tam giác ade cân a
=> góc d = góc e và ad = ae
tam giác adb = tam giác aec ( cgc)
=> ab=ac
=> tam giác abc cân a
b, tam giác bmd vuông m và tam giác cne vuông n
góc m = góc n =90 độ
góc d = góc e
bd = ce
=> bmd = cne (ch-gn)
=> bm = cn
c, có tam giác bmd = tam giác cne
=> góc mbd = góc nce
mà góc cbi đối đỉnh góc mbd, bci đối đỉnh nce
=> góc cbi = góc bci
=> tam giác ibc cân i
d, lây h là trung điểm bc
tam giác abc cân a có ah là đường trung tuyến úng với bc
=> ah vừa là trung tuyến vừa là đường cao ứng với bc
cmtt với ibc => ih vừa là trung tuyến vừa là đường cao ứng với bc
=> a,i,h thẳng hàng
=> ai vừa trung tuyến vừa là đường cao tam giác abc cân a
=> đpcm

ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b