Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn gốc thời gian là khi trạng thái dao động của hệ như hình vẽ → phương trình dao động của vật và hình chiếu của S theo phương ngang Ox là:

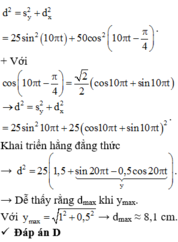

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Đáp án C
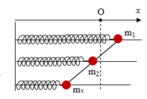
Ta có ω 1 = ω 2 = ω 3 = 10 π rad / s
Phương trình dao động của vật 1 và vật 2 là:
x 1 = 3 cos ( 10 πt - π 2 ) c m x 2 = 1 , 5 cos ( 10 πt ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = ± A )
Trong quá trình dao động cả ba vật nằm trên một đường thẳng khi 2 x 2 = x 1 + x 3 ⇒ x 3 = 2 x 2 - x 1
tính chất trung bình
Bấm máy tính tổng hợp dao động ta được
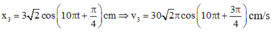
Taị t = 0 và v 30 = - 30 π cm / s
Trường hợp x 2 = 1 , 5 cos ( 10 π t + π ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = - A )
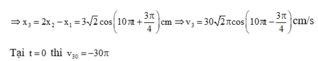

Đáp án B
Công suất tức thời của lực đàn hồi: P = F.v = k.x. ω . A 2 - x 2
Theo Cô-si ta có:
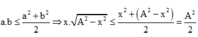
Suy ra: P ≤ k . ω . A 2 2 ⇒ P m a x = k . ω . A 2 2
Thay v m a x = A . ω v à o t a được
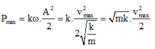
Thay số vào ta được: P m a x = m . k . v m a x 2 2 = 0 , 5 . 50 . 1 2 2 = 2,5 W

Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 1 cm.
Tần số góc dao động của con lắc ω = k m = 10 10 rad/s.
+ Vận tốc truyền cho vật m so với điểm treo có độ lớn v 0 = 10 + 40 = 50 cm/s.
→ Biên độ dao động của vật sau đó A = v 0 ω = 50 10 10 = 1 , 58 cm.
→ Chiều dài cực đại l m a x = l 0 + Δ l 0 + A = 27 , 58 c m .

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5

Chọn A
+ Động năng bằng thế năng ở vị trí x = ±A√2/2 = ±√2 cm và v = ωA/√2 = 6π cm.
+ Khi mo rơi và dính vào m, theo định luật bảo toàn động lượng (chú ý là vật m0 rơi thẳng đứng nên động lượng của nó theo phương ngang = 0): (m+mo)v’ = mv => v’ = 4π cm/s.
+ Hệ (m + mo) có ω’ = 2π√3 rad/s và qua VTCB vận tốc của hệ là:
![]()
![]()
![]()

Đáp án A
Khi vật đang ở vị trí cân bằng ta tác dụng vào nó một lực F có độ lớn không đổi theo phương trục lò xo
⇒ v m a x = F m k
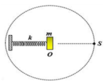
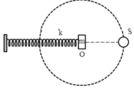
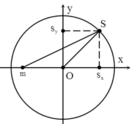
- S chuyển động tròn đều trên đường tròn tâm O bán kính 5cm với tốc độ góc 10π (rad/s)
- Vật m dao động điều hoà với với:
Tốc độ cực đại của m là : vmax = ωA = 50π cm/s => A = 5cm.
- Tại thời điểm nào đó, điểm sáng S đang đi qua vị trí như trên hình vẽ, còn vật nhỏ m đang có tốc độ cực đại (m có tốc độ cực đại khi qua vị trí cân bằng) => S và m luôn lệch pha nhau góc π/2.
S và m cách nhau lớn nhất khi m và S đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có :
Áp dụng định lí Py – ta – go, ta có khoảng cách lớn nhất giữa S và m (đường màu đỏ) là :
Đáp án D