Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
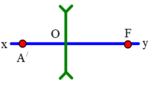
Nối A’ với C kéo dài cắt xy tại G thì G chính là A’ tiêu điểm chính ảnh của thấu kính

Đáp án B
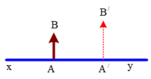
Nối B T kéo dài cắt xy tại N thì N là tiêu điểm chính ảnh

Đáp án cần chọn là: A
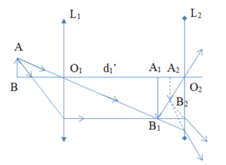
+ Qua L 1 vật AB có ảnh A 1 B 1 cách L 1 là:
d 1 ' = d 1 f 1 d 1 − f 1 = 15.10 15 − 10 = 30 c m
Số phóng đại k 1 = − d 1 ' d 1 = − 30 15 = − 2
+ Hình vẽ cho thấy, A 1 B 1 cách thấu kính L 2 một đoạn:
d 2 = a − d 1 ' = 40 − 30 = 10 c m
+ Ánh sáng truyền qua L 1 hội tụ tại A 1 B 1 rồi lại truyền tiếp tới L 2 .
Do vậy A 1 B 1 lại là vật sáng đối với L 2 .
+ Vận dụng công thức thấu kính với L 2 , ta được:
d 2 ' = d 2 f 2 d 2 − f 2 = 10. ( − 10 ) 10 + 10 = − 5 c m
k 2 = − d 2 ' d 2 = 1 2
+ Số phóng đại ảnh của hệ thấu kính:
k = A 2 B 2 ¯ A B ¯ = A 2 B 2 ¯ A 1 B 1 ¯ . A 1 B 1 ¯ A B ¯ = k 2 . k 1
k = − 1
+ Vậy ảnh cuối cùng của hệ là ảnh ảo, cao bằng vật, ngược chiều với vật, cách L 2 một đoạn 5cm

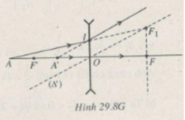
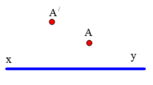
- Vẽ tia ló theo A’l (bất kỳ)
- Dựng trục phụ ( ∆ ’) song song với tia ló và xác định tiêu điểm vật phụ F 1
- Vẽ tia tới có đường kéo dài là I F 1 . Tia này cắt trục chính tại A: vật điểm (Hình 29.8G).

Chọn đáp án D.
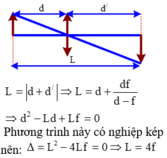
Theo bài ra ta có: d + d’ = L nên d’ = L – d
Mặt khác:
1 f = 1 d + 1 d ' ⇔ 1 f = 1 d + 1 L − d ⇔ d L − d = L f ⇔ d 2 − L d + L f = 0 (*)
Vì chỉ có một vị trí duy nhất của thấu kính tại đó có ảnh của vật hiện lên rõ nét trên màn nên phương trình (*) có nghiệm duy nhất ⇔ Δ = L 2 − 4 L f = 0 ⇔ f = L 4 = 5 c m .

Theo đề: l = d2 - d1 = √Δ
Ta có: 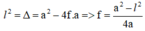
∗ Vậy muốn tìm tiêu cự của thấu kính ta dùng thí nghiệm để tìm được hai vị trí của thấu kính cho ảnh rõ trên màn. Sau đó:
- Đo khoảng cách vật – màn bằng a.
- Đo khoảng cách l giữa hai vị trí của thấu kính cho ảnh rõ nét trên màn.
- Áp dụng công thức: 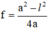


a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!
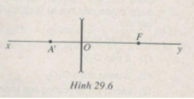
Đáp án C
Qua O kẻ trục phụ Δ. Từ F kẻ đường vuông góc với xy cắt A tại F1. Qua A’ kẻ đường song song với A cắt thấu kinh tại I. Nối F1I cắt xy tại A