Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
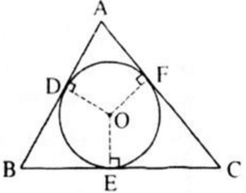
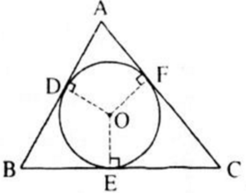
a, Tam giác ABC ngọi tiếp đường tròn \(\left(O\right)\)nên AB, BC, AC lần lượt là tiếp tuyến tại D, E , F của đường tròn.
Theo tính chất của hai đường tiếp tuyến cắt nhau, ta có:
AD = AF ; DB = BE ; FC = CE
Xét vế phải:
VP = AB + AC - BC
= ( AD + DB ) + ( AF + CF ) - ( BE + CE )
Thay DB = BE , FC = CE vào biểu thức trên, ta được:
VP = ( AD + BE ) + ( AF + CE ) - ( BE + CE )
= AD + BE + AF + CE - BE - CE
= ( AD + AF ) + ( BE - BE ) + ( CE - CE )
= AD + AF
= AD + AD = 2AD
Vậy 2AD = AB + AC - BC
b, Các hệ thức tương tự là:
2BD = BA + BC - AC
2CF = CA + CB - AB
Cách 1: Đặt tên các đoạn thẳng như hình bên.
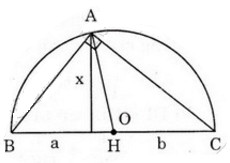
Ta có:
.
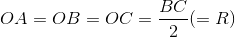Suy ra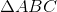 
vuông tại A.
Áp dụng hệ thức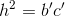 
ta có: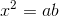 
Cách 2:
Cũng chứng minh 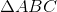vuông như cách 1.
Áp dụng hệ thức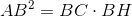 
ta được .
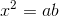a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)
b) Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
AD=AF; BD=BE; CF=CE.
Xét vế phải AB+AC-BC=
=(AD+DB)+(AF+FC)-(BE+EC)
=(AD+BE)+(AF+CE)-(BE+EC)
= AD+AF=2AD.
b) Các hệ thức tương tự là:
2BD=BA+BC-AC;
2CF=CA+CB-AB.
Nhận xét. Từ bài toán trên ta có các kết quả sau:
AD=AF=p-a; BD=BE=p-b; CE=CF=p-c
trong đó AB=c; BC=a; CA=b và p là nửa chu vi của tam giác ABC.
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
AD=AF; BD=BE; CF=CE.
Xét vế phải AB+AC-BC=
=(AD+DB)+(AF+FC)-(BE+EC)
=(AD+BE)+(AF+CE)-(BE+EC)
= AD+AF=2AD.
b) Các hệ thức tương tự là:
2BD=BA+BC-AC;
2CF=CA+CB-AB.
Nhận xét. Từ bài toán trên ta có các kết quả sau:
AD=AF=p-a; BD=BE=p-b; CE=CF=p-c
trong đó AB=c; BC=a; CA=b và p là nửa chu vi của tam giác ABC.
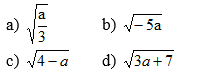
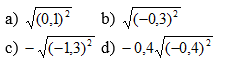
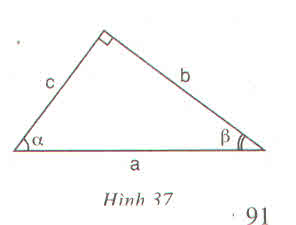
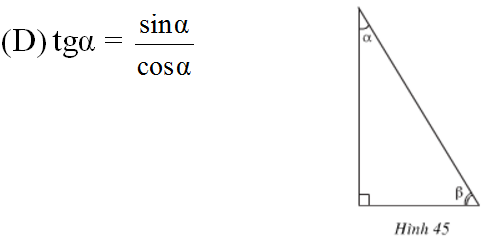
Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB