Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

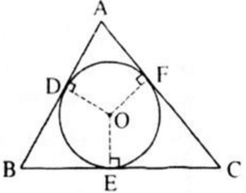
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)
b) Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB

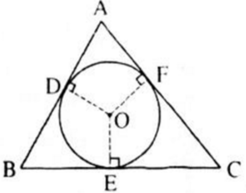
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
AD=AF; BD=BE; CF=CE.
Xét vế phải AB+AC-BC=
=(AD+DB)+(AF+FC)-(BE+EC)
=(AD+BE)+(AF+CE)-(BE+EC)
= AD+AF=2AD.
b) Các hệ thức tương tự là:
2BD=BA+BC-AC;
2CF=CA+CB-AB.
Nhận xét. Từ bài toán trên ta có các kết quả sau:
AD=AF=p-a; BD=BE=p-b; CE=CF=p-c
trong đó AB=c; BC=a; CA=b và p là nửa chu vi của tam giác ABC.
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
AD=AF; BD=BE; CF=CE.
Xét vế phải AB+AC-BC=
=(AD+DB)+(AF+FC)-(BE+EC)
=(AD+BE)+(AF+CE)-(BE+EC)
= AD+AF=2AD.
b) Các hệ thức tương tự là:
2BD=BA+BC-AC;
2CF=CA+CB-AB.
Nhận xét. Từ bài toán trên ta có các kết quả sau:
AD=AF=p-a; BD=BE=p-b; CE=CF=p-c
trong đó AB=c; BC=a; CA=b và p là nửa chu vi của tam giác ABC.

Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB

Vì nếu hai đường tròn tiếp xúc ngoài thì hai bánh xe quay theo hai chiều khác nhau (một bánh xe quay cùng chiều quay của kim đồng hồ, bánh xe kia quay ngược chiều của kim đồng hồ). Nếu hai đường tròn tiếp xúc trong thì hai bánh xe quay theo chiều như nhau. Do đó:
- Hình a, b hệ thống bánh răng chuyển động được.
- Hình c, hệ thống bánh răng không chuyển động được.
Vì nếu hai đường tròn tiếp xúc ngoài thì hai bánh xe quay theo hai chiều khác nhau (một bánh xe quay cùng chiều quay của kim đồng hồ,bánh xe kia quay ngược chiều kim đồng hồ).Nếu hai đường tròn tiếp xúc trong thì hai bánh xe quay theo chiều như nhau.Do đó:
- Hình a,b hệ thống bánh răng chuyển động được.
- Hình c hệ thống bánh răng không chuyển động được.
nhớ tk mk nha

Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)

Tam giác ABCABC có:
AB^2+AC^2=3^{2}+4^{2}=5^{2}AB2+AC2=32+42=52
Mặt khác: BC^{2}=5^{2}BC2=52
Vậy \mathrm{AB}^{2}+\mathrm{AC}^{2}=\mathrm{BC}^{2}AB2+AC2=BC2.
Do đó \widehat{BAC}=90^{\circ}BAC=90∘ (định lí Py-ta-go đảo).
CACA vuông góc với bán kính BABA tại AA nên CACA là tiếp tuyến của đường tròn (B)(B).

Bạn tự vẽ hình nha
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // OI (OI là đường trung bình của tam giác BCD).
Vậy BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
AC^2 = OA^2 – OC^2 = 42 – 22 = 12
=> AC = √12 = 2√3 (cm)
\(\sin OAC=\frac{OC}{OA}=\frac{1}{2}\)
=> OAC =30 độ
mà BAC =2OAC
=. BAC =60
Tam giác ABC cân có BAC = 60 => Tam giác ABC đều
+> AB=AC=BC=2√3 (cm)
K cho mk nh
câu A : AB = AC ( theo tính chất của đường tiếp tuyến ) suy ra : tam giác ABC cân tại A , OA là đường phân giác cũng là đường cao vậy OA vuông góc với BC

Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)

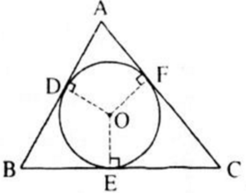
a, Tam giác ABC ngọi tiếp đường tròn \(\left(O\right)\)nên AB, BC, AC lần lượt là tiếp tuyến tại D, E , F của đường tròn.
Theo tính chất của hai đường tiếp tuyến cắt nhau, ta có:
AD = AF ; DB = BE ; FC = CE
Xét vế phải:
VP = AB + AC - BC
= ( AD + DB ) + ( AF + CF ) - ( BE + CE )
Thay DB = BE , FC = CE vào biểu thức trên, ta được:
VP = ( AD + BE ) + ( AF + CE ) - ( BE + CE )
= AD + BE + AF + CE - BE - CE
= ( AD + AF ) + ( BE - BE ) + ( CE - CE )
= AD + AF
= AD + AD = 2AD
Vậy 2AD = AB + AC - BC
b, Các hệ thức tương tự là:
2BD = BA + BC - AC
2CF = CA + CB - AB
a) AB+AC-BCAB+AC−BC
=(AD+BD)+(AF+FC)-(BE+EC)=(AD+BD)+(AF+FC)−(BE+EC)
=(AD+AF)+(BD-BE)+(FC-EC)=(AD+AF)+(BD−BE)+(FC−EC)
Do BD=BE, FC=EC, AD=AFBD=BE,FC=EC,AD=AF nên
AB+AC-BC=2ADAB+AC−BC=2AD.
b) 2 BE=BA+BC-AC2BE=BA+BC−AC
2 CF=CA+CB-AB2CF=CA+CB−AB.