Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=3x^2-6x+m\)
để hàm số đồng biến trên R thì y'>0 với mọi x thuộc R
suy ra \(\begin{cases}3>0\\\Delta=9-3m<0\end{cases}\) suy ra m>3
vậy m>3 là điều cần tìm

+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |

Đáp án là B.
Ta có y ' ( x ) = ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1
TH1. m - 1 = 0 ⇔ m = 1 .Khi đó
y , = - 1 < 0 , ∀ x ∈ ℝ .Nên hàm só luôn nghịch biếến trên ℝ .
TH2. m - 1 ≢ 0 ⇔ m ≢ 1 .Hàm số luôn nghịch biến trên ℝ khi
y , ≤ 0 , ∀ x ∈ ℝ ⇔ ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1 ≤ 0 , ∀ x ∈ ℝ ⇔ m - 1 < 0 ∆ ' ≤ 0 ⇔ m < 1 m ( m - 1 ) ≤ 0 ⇔ 0 ≤ m ≤ 1 . Kết hợp ta được 0 ≤ m < 1 .

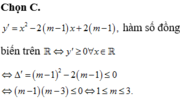
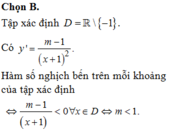

Đáp án D
Với y = ( m - 2 ) x 3 + ( m - 2 ) x 2 - x + 1 ta có y ' = 3 ( m - 2 ) x 2 + 2 ( m - 2 ) x - 1
Hàm số đã cho nghịch biến trên R
⇔ m - 2 < 0 ∆ ' ≤ 0 ⇔ m < 2 m 2 - m - 2 ≤ 0 ⇔ m < 2 - 1 ≤ m ≤ 2 ⇔ 1 ≤ m ≤ 2