Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
\(|x|=2019\Rightarrow \left[\begin{matrix} x=2019\\ x=-2019\end{matrix}\right.\)
b)
\(|x-3|=21\Rightarrow \left[\begin{matrix} x-3=21\\ x-3=-21\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=24\\ x=-18\end{matrix}\right.\)
c)
\(|x|-25+x=9\)
\(\Leftrightarrow |x|+x=34\)
Nếu $x\geq 0$: $|x|=x$
\(\Rightarrow x+x=34\Rightarrow 2x=34\Rightarrow x=17\) (thỏa mãn)
Nếu $x< 0$: $|x|=-x$
$\Rightarrow -x+x=34\Rightarrow 0=34$ (vô lý -loại)
Vậy $x=17$
d) \(|x-2|+2x=4\)
Nếu $x\geq 2\Rightarrow |x-2|=x-2$
$\Rightarrow x-2+2x=4\Rightarrow 3x=6\Rightarrow x=2$ (thỏa mãn)
Nếu $x< 2\Rightarrow |x-2|=2-x$
$\Rightarrow 2-x+2x=4\Rightarrow x=2$ (loại vì $x< 2$)
Vậy $x=2$
e)
$|x-5|+3x+2=13$
Nếu $x\geq 5$ thì $|x-5|=x-5$
\(\Rightarrow x-5+3x+2=13\)
\(\Leftrightarrow 4x=16\Leftrightarrow x=4\) (loại vì $x\geq 5$)
Nếu $x< 5$ thì $|x-5|=5-x$
$\Rightarrow 5-x+3x+2=13$
$\Leftrightarrow 2x=6\Rightarrow x=3$ (thỏa mãn)
Vậy $x=3$

\(\left(x+\frac{1}{5}\right)^2+\frac{17}{25}=\frac{26}{25}\\ \left(x+\frac{1}{5}\right)^2=\frac{26}{25}-\frac{17}{25}\\ \left(x+\frac{1}{5}\right)^2=\frac{9}{25}\\ \left|\left(x+\frac{1}{5}\right)\right|=\frac{3}{5}\)
TH1: \(x=\frac{3}{5}-\frac{1}{5}\\ x=\frac{2}{5}\)
TH2: \(\left|\left(x+\frac{1}{5}\right)\right|=-\frac{3}{5}\\ x=-\frac{3}{5}-\frac{1}{5}\\ x=-\frac{4}{5}\)
\(a,\left(x+\frac{1}{5}\right)^2+\frac{17}{25}=\frac{26}{25}\)
\(\Rightarrow\left(x+\frac{1}{5}\right)^2=\frac{9}{25}\)
\(\Rightarrow\left(x+\frac{1}{5}\right)^2=\left(\frac{3}{5}\right)^2\)
\(\Rightarrow x+\frac{1}{5}=\frac{3}{5}\)
\(\Rightarrow x=\frac{2}{5}\)
\(b,-1\frac{5}{27}-\left(3x-\frac{7}{9}\right)^3=-\frac{24}{27}\)
\(\Rightarrow-\frac{32}{27}-\left(3x-\frac{7}{9}\right)^3=-\frac{24}{27}\)
\(\Rightarrow\left(3x-\frac{7}{9}\right)^3=-\frac{32}{27}+\frac{24}{27}\)
\(\Rightarrow\left(3x-\frac{7}{9}\right)^3=-\frac{8}{27}\)
\(\Rightarrow\left(3x-\frac{7}{9}\right)^3=\left(-\frac{2}{3}\right)^3\)
\(\Rightarrow3x-\frac{7}{9}=-\frac{2}{3}\)
\(\Rightarrow3x=-\frac{2}{3}+\frac{7}{9}\)
\(\Rightarrow3x=\frac{1}{9}\)
\(\Rightarrow x=\frac{1}{27}\)
\(c,\left(x+\frac{1}{2}\right)\left(\frac{2}{3}-2x\right)=0\)
\(\Rightarrow\) \(\left[\begin{array}{nghiempt}x+\frac{1}{2}=0\\\frac{2}{3}-2x=0\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}x=-\frac{1}{2}\\2x=\frac{2}{3}\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}x=-\frac{1}{2}\\x=\frac{1}{3}\end{array}\right.\)

\(A=\left|-x+8\right|-21\)
\(A=\left|-x+8\right|-21\ge-21\)
\(MinA=-21\Leftrightarrow-x+8=0\)\(\Leftrightarrow x=8\)
\(B=\left|-x-17\right|+\left|y-36\right|+12\)
\(B=\left|-x-17\right|+\left|y-36\right|+12\ge12\)
\(MinB=12\Leftrightarrow\hept{\begin{cases}-x-17=0\\y-36=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-17\\y=36\end{cases}}\)
\(C=-\left|2x+8\right|-35\)
\(C=-\left|2x+8\right|-35\le-35\)
\(MaxC=-35\Leftrightarrow2x+8=0\Leftrightarrow x=-4\)

Dạng 3 :
a) 3x - 10 = 2x + 13
=> 3x - 2x = 13 - 10
=> x = 3
b) x + 12 = -5 - x
=> x + x = -5 - 12
=> 2x = -17
=> x = -8,5
c) x + 5 = 10 - x
=> x + x = 10 - 5
=> 2x = 5
=> x = 2,5
d) 6x + 23 = 2x - 12
=> 2x - 6x = 23 + 12
=> -4x = 35
=> x = -8,75
e) 12 - x = x + 1
=> x + x = 12 - 1
=> 2x = 11
=> x = 5,5
f) 14 + 4x = 3x + 20
=> 4x - 3x = 20 - 14
=> x = 6

\(\text{a) A = | -x + 8| - 21}\)
Vì | -x + 8| \(\le\) 0 ( với mọi x )
=> A = | -x + 8| - 21\(\ge\) -21
=> Amax = -21 khi | -x + 8| = 0 => -x + 8 = 0 => -x = -8 => x = 8
Vậy với Amin = -21 thì x = 8
b) \(B=\left|-x-17\right|+\left|y-36\right|+12\)
Vì \(\left\{\begin{matrix}\left|-x-17\right|\ge0\\\left|y-36\right|\ge0\end{matrix}\right.\)=> \(\left|-x-17\right|+\left|y-36\right|\ge0\)
=> \(B=\left|-x-17\right|+\left|y-36\right|+12\le12\)
=> Bmin = 12 khi \(\left|-x-17\right|+\left|y-36\right|=0\)
=> \(\left\{\begin{matrix}\left|-x-17\right|=0\\\left|y-36\right|=0\end{matrix}\right.\)=> \(\left\{\begin{matrix}-x-17=0\\y-36=0\end{matrix}\right.\)=> \(\left\{\begin{matrix}-x=17\\y=36\end{matrix}\right.\)=>\(\left\{\begin{matrix}x=-17\\y=36\end{matrix}\right.\)
Vậy Bmin = 12 khi \(\left\{\begin{matrix}x=-17\\y=36\end{matrix}\right.\)
c) \(C=-\left|2x-8\right|-35\)
Vì \(-\left|2x-8\right|\ge0\)
=> \(C=-\left|2x-8\right|-35\ge-35\)
=> Cmin = -35 khi \(-\left|2x-8\right|=0\)=> \(-2x-8=0\)=>\(-2x=8\)=> \(x=4\)
Vậy Cmin = -35 khi x = 4
d) \(D=3\left(3x-12\right)^2-37\)
Vì \(\left(3x-12\right)^2\ge0\)
=> \(3\left(3x-12\right)^2\ge0\)
=> \(D=3\left(3x-12\right)^2-37\ge-37\)
=> Dmin = -37 khi \(3\left(3x-12\right)^2=0\) => \(\left(3x-12\right)^2=0\)=> \(3x-12=0\)=> \(3x=12\)=>\(x=4\)
Vậy Dmin = -37 khi x = 4
a, A=|-x+8|-21
Vì |-x+8|>hoặc =0 với mọi x
suy ra |-x+8|-21>hoặc = -21
Dấu = xảy ra khi và chỉ khi |-x+8|=0
Khi và chỉ khi -x+8=0
Khi và chỉ khi-x=-8
khi và chỉ khi x =8
Vậy GTNN của A là -21 tại x=8
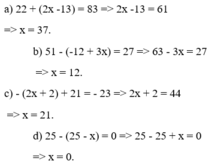
a) 22 + (2x -13) = 83 => 2x -13 = 61 => x = 37.
b) 51 - (-12 + 3x) = 27 => 63 - 3x = 27 => x = 12.
c) - (2x + 2) + 21 = - 23 => 2x + 2 = 44 => x = 21.
d) 25 - (25 - x) = 0 => 25 - 25 + x = 0 => x = 0.