Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)

Nếu F1=F2
do góc giữa vecto F1, F2=60o
áp dụng định lý hàm cos
F2=F12+ F22+2F1F2cos (vecto)
=> F1=0,58F
|
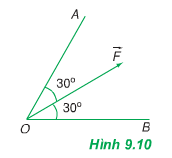
Phân tích lực F→F→ thành hai lực F1−→F1→ và F2−→F2→ theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần? A. F1 = F2 = F; B. F1 = F2 = 1212F; C. F1 = F2 = 1,15F; D. F1 = F2 = 0,58F. |

Hình như bạn nhầm nơi rồi đấy đây là BOX Lí mà đăng HÓA

1.
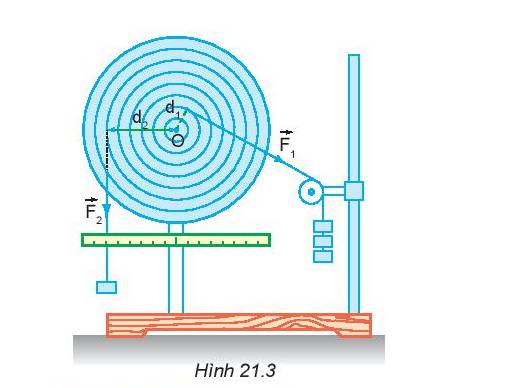
Nếu bỏ lực \(\overrightarrow {{F_1}} \) thì đĩa quay ngược chiều kim đồng hồ.
2.
Nếu bỏ lực \(\overrightarrow {{F_2}} \) thì đĩa quay theo chiều kim đồng hồ

a. Chọn hệ quy chiếu thẳng đứng
AFk = F.s = P.s = mg.s = 3.10.1,5 = 45 J
b. Mình chưa hiểu đề ?
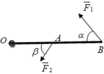

Theo điều kiện cân bằng của Momen lực
M F → 1 = M F → 2 ⇒ F 1 . d F 1 = F 2 . d F 2 ⇒ F 1 . O B . sin α = F 2 . O A . sin β
Mà OB = OA + AB =50 ( cm )
a. Khi a= β= 90o ta có
⇒ 20.0 , 5. s i n 90 0 = F 2 .0 , 1. sin 90 0 ⇒ F 2 = 100 ( N )
b. Khi a= 30o; β= 90o ta có
⇒ 20.0 , 5. s i n 30 0 = F 2 .0 , 1. sin 90 0 ⇒ F 2 = 50 ( N )
c. Khi a= 30o; β= 60o ta có
⇒ 20.0 , 5. s i n 30 0 = F 2 .0 , 1. sin 60 0 ⇒ F 2 = 100 3 N