
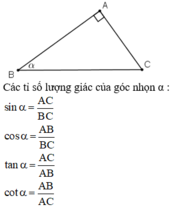
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



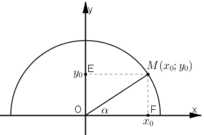
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho 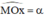
Khi đó ta có:
sin α = y0
cos α = x0
tan α = y0 / x0
cot α = x0 / y0
b) Gọi E, F là hình chiếu của M trên Oy, Ox.
Khi α < 90º thì x0 > 0, y0 > 0
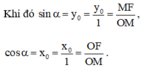

Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.

A B C M N I
Gọi I là giao điểm MB, CN thì I là trọng tâm tam giác
\(sin\widehat{ACN}=\dfrac{AB}{2CN}=\dfrac{AB}{\sqrt{4AC^2+AB^2}}\) ; \(BM=\sqrt{\dfrac{AC^2}{4}+AB^2}\Rightarrow IM=\dfrac{1}{3}\sqrt{\dfrac{AC^2}{4}+AB^2}\)
Ta có: \(\dfrac{sin\widehat{CIM}}{CM}=\dfrac{sin\widehat{ACN}}{IM}\Leftrightarrow sin\alpha=\dfrac{CM}{IM}sin\widehat{ACN}=\dfrac{AC}{\dfrac{2}{3}\sqrt{\dfrac{AC^2}{4}+AB^2}}.\dfrac{AB}{\sqrt{4AC^2+AB^2}}\)
\(\Leftrightarrow sin\alpha=\dfrac{3AB.AC}{\sqrt{\left(4AB^2+AC^2\right)\left(4AC^2+AB^2\right)}}\le\dfrac{3AB.AC}{5AB.AC}=\dfrac{3}{5}\)

AM vuông góc với DE chứ.
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right);\overrightarrow{DE}=\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{DE}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}.\overrightarrow{AE}-\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left[AB.AE.cos\left(\widehat{BAC}+90^o\right)-AC.AD.cos\left(\widehat{BAC}+90^o\right)-AB.AD.cos90^o+AC.AE.cos90^o\right]\)
\(=0\)
\(\Rightarrow AM\perp DE\)

Gọi G là giao điểm BM và CN. Đặt AB=c, AC=b
Ta có: \(BM^2=\dfrac{2\left(a^2+c^2\right)-b^2}{4}\) ; \(\Rightarrow BG^2=\left(\dfrac{2}{3}BM\right)^2=\dfrac{2\left(a^2+c^2\right)-b^2}{9}\)
\(CN^2=\dfrac{2\left(a^2+b^2\right)-c^2}{4}\Rightarrow CG^2=\dfrac{2\left(a^2+b^2\right)-c^2}{9}\)
Mặt khác \(BG^2+CG^2=BC^2\)
\(\Rightarrow\dfrac{2\left(a^2+c^2\right)-b^2}{9}+\dfrac{2\left(a^2+b^2\right)-c^2}{9}=a^2\)
\(\Rightarrow b^2+c^2=5a^2\)
Áp dụng định lý hàm cos:
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{5a^2-a^2}{2bc}=\dfrac{2a^2}{bc}\Rightarrow bc=\dfrac{2a^2}{cos\alpha}\)
\(S_{ABC}=\dfrac{1}{2}bcsinA=\dfrac{1}{2}.\dfrac{2a^2}{cos\alpha}.sin\alpha=a^2.tan\alpha\)