Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

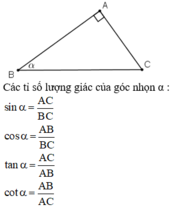
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.

Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy
=> = cosα;
=
= sinα;
Trong tam giác vuông MPO:
MP2+ PO2 = OM2 => cos2 α + sin2 α = 1

a) \(sin120^o=sin60^o=\dfrac{\sqrt{3}}{2};cos120^o=-cos60^o=-\dfrac{1}{2}\);
\(tan120^o=-\sqrt{3};cot120^o=\dfrac{-1}{\sqrt{3}}\).
b) \(sin150^o=sin30^o=\dfrac{1}{2};cos150^o=-cos30^o=-\dfrac{\sqrt{3}}{2}\).
\(tan150^o=-tan30^o=-\dfrac{\sqrt{3}}{3}\); \(cot150^o=-cot30^o=-\sqrt{3}\).
c)\(sin135^o=sin45^o=\dfrac{\sqrt{2}}{2};cos135^o=-cos45^o=-\dfrac{\sqrt{2}}{2}\).
\(tan135^o=-tan45^o=-1\); \(cot135^o=-1\).

Em 2k8 ms học nên k chắc
Vì 0 < \(\alpha< \dfrac{\pi}{2}\) => sin \(\alpha>0\)
Cos \(\alpha=\dfrac{1}{3}\) \(\Rightarrow sin\alpha=\sqrt{1-\dfrac{1}{9}}=\dfrac{2\sqrt{2}}{3}\)
tan \(\alpha=2\sqrt{2}\) ; cot \(\alpha=\dfrac{1}{2\sqrt{2}}\)

Với 0 < α < π/2 thì cosα >0, sinα >0. Ta có
1 - sin 2 α = cos 2 α
Mặt khác cos 2 α = ( 2 sin α ) 2 = 4 sin 2 α nên 5 sin 2 α = 1 hay
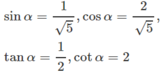

a)\(\sin^2\alpha+\cos^2\alpha=1\Rightarrow\sin^2\alpha=1-\cos^2\alpha\)
\(\Rightarrow1-2^2=-3\) \(\Rightarrow\cos=-\sqrt{3}\left(0< \alpha< \dfrac{\pi}{2}\right)\)
b) \(\tan\alpha\times\cot\alpha=1\Rightarrow\tan\alpha=\dfrac{1}{\cot\alpha}\Rightarrow\tan=\dfrac{1}{4}\)
a)Do \(0< \alpha< \dfrac{\pi}{2}\) nên các giá trị lượng giác của \(\alpha\) đều dương.
\(cos\alpha=2sin\alpha\)(1)
Nếu \(sin\alpha=0\Rightarrow cos\alpha\) (vô lý).
Vì vậy \(sin\alpha\ne0\) . Từ (1) \(\Rightarrow\dfrac{cos\alpha}{sin\alpha}=2\)\(\Leftrightarrow cot\alpha=2\).
Suy ra: \(tan\alpha=\dfrac{1}{2}\).
\(sin\alpha=\sqrt{\dfrac{1}{1+cot^2\alpha}}=\dfrac{1}{\sqrt{3}}\).
\(cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{\dfrac{2}{3}}\).
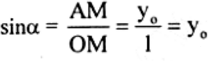
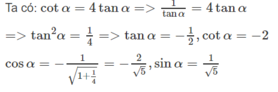
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho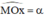
Khi đó ta có:
sin α = y0
cos α = x0
tan α = y0 / x0
cot α = x0 / y0
b) Gọi E, F là hình chiếu của M trên Oy, Ox.
Khi α < 90º thì x0 > 0, y0 > 0