Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Trong tam giác vuông A’B’C’ có \(\widehat{A'}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
A′B′2+A′C′2 =B′C′2
=> A′C′2=B′C′2−A′B′2=152−92=144
=> A’C’ =12 (cm)
Trong tam giác vuông ABC có \(\widehat{A}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
BC2=AB2+AC2= 62+82=100
Suy ra: BC = 10 (cm)
Ta có: \(\dfrac{A'B'}{AB}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(\dfrac{A'C'}{AC}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\dfrac{B'C'}{BC}=\dfrac{15}{10}=\dfrac{3}{2}\)
Suy ra: \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}=\dfrac{3}{2}\)
Vậy ∆ A’B’C’ đồng dạng với ∆ ABC

A B C 9 12 D E
a, Xét tam giác ABC và tam giác EDC ta có :
^C _ chung
\(\frac{BC}{DC}=\frac{AC}{EC}\)
^BAE = ^CED = 90^0
=> tam giác ABC ~ tam giác CED ( g.c.g )
HAB ? ^H ở đâu bạn ?
b, Vì AD là tia phân giác tam giác ABC ta có :
\(\frac{AB}{AC}=\frac{BD}{DC}\Leftrightarrow\frac{9}{12}=\frac{BD}{DC}\)
hay \(\frac{BD}{DC}=\frac{9}{12}\)tự tính BD và CD nhé
c, Vì AB vuông AC ; DE vuông AC => AB // DE. Áp dụng hệ quả Ta lét :
\(\frac{CE}{BC}=\frac{DE}{AB}\)thay dữ liệu bên phần b tính
d, Áp dụng Py ta go với dữ kiện bên trên tìm tí số

Giải:
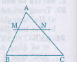
Trên cạnh AB lấy điểm M sao cho AM= 2323AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=2323
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)

Ta có : \(\frac{\Delta_{ABC}}{\Delta_{DÈF}}=\frac{3}{5}\Rightarrow\frac{12}{\Delta_{DEF}}=\frac{3}{5}\)
\(\Rightarrow\Delta_{DEF}=\frac{3}{5}:\frac{1}{12}=\frac{36}{5}=7,2\)cm
Vậy chu vi tam giác DEF là 7,2 m

\(\text{Ta có:}\)\(\Delta ABC\text{∽}\Delta DEF\)\(\text{theo tỉ số đồng dạng}\)\(k=\frac{3}{5}\)
\(\text{Nửa chu vi}\)\(\Delta ABC\)\(=\)\(\text{nửa chu vi}\)\(\Delta DEF=\frac{3}{5}\)
\(\text{Mà chu vi}\)\(\Delta ABC=12cm\)
\(\text{Nửa chu vi}\)\(\Delta ABC\)\(:\)\(12:2=6cm\)
\(\text{Nửa chu vi}\)\(\Delta DEF\)\(:\)\(6:\frac{3}{5}=10cm\)
\(\text{Chu vi}\)\(\Delta DEF\)\(:\)\(10.2=20cm\)
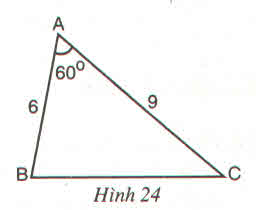





* Cách dựng:
- Trên cạnh AB dựng điểm B' sao cho = 2 cm
- Trên cạnh AC dựng điểm C' sao cho AC' = 3cm
- Nối B'C'
Khi đó AB'C' là tam giác cần dựng
* Chứng minh:
Theo cách dựng, ta có:
Suy ra: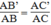
Lại có: ∠ A chung
Vậy △ AB'C' đồng dạng △ ABC (c.g.c)