Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
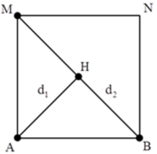
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Chọn đáp án B
x A M = A c os ( ω t − 2 π d 1 λ ) x B M = A cos ( ω t + π − 2 π d 1 λ )
phương trình sóng tại M
x M = x A M + x B M = − 2 A sin d 2 + d 1 λ . sin ( ω t − d 2 + d 1 λ π )
Biên độ sóng tại M: A M = 2 A sin d 2 − d 1 λ π ; tại M nếu A M = A 2
⇒ sin d 2 − d 1 λ π = ± 1 2 ⇒ d 2 − d 1 λ π = π 4 + k π 2 ⇒ d 2 − d 1 = λ 4 + k λ 2
Xét trên AB
d 2 A − d 1 A ≤ d 2 − d 1 ≤ d 2 B − d 1 B ⇔ − A B ≤ λ 4 + k λ 2 ≤ A B
Ta có: f = ω 2 π = 10 H z ; λ = v t = 3 c m
⇒ − 20,5 ≤ k ≤ 19,5 ⇒ k = 0, ± 1, ± 2... ± 19, − 20
⇒ có 40 điểm.

Đáp án A
+ Bước sóng của sóng λ = 2 π v ω = 1 , 6 c m
Xét tỉ số 2 S 1 S 2 λ = 15 ⇒ có 30 điểm dao động với biên độ 3mm

Đáp án B
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì:
d 1 - d 2 = ( k + 1 2 ) λ
+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số d1 – d2:
AM - 2 AM ≤ d 1 - d 2 ≤ AB
+ Kết hợp hai phương trình trên ta thu được:
AM ( 1 - 2 ) λ - 1 2 ≤ k ≤ A B λ - 1 2
→ - 6 , 02 ≤ k ≤ 12 , 8
Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.

Đáp án: A
HD Giải: λ = 80 2 π 100 π = 1,6cm
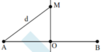
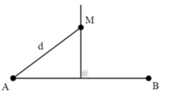
M cùng pha với nguồn A nên MA = d = (được rút ra từ phương trình sóng tại M với d1 = d2 = d)
Ta có điều kiện MA > AO = AB/2 nên
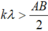
<=> 1,6k > 6
<=> k > 3,75
MA nhỏ nhất nên chọn k = 4
MA = 4.1,6 = 6,4 cm
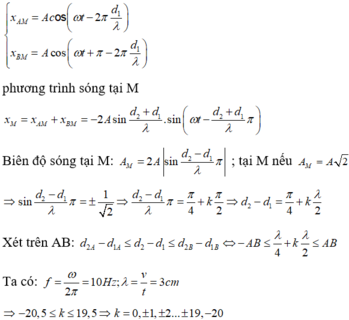


Đáp án A
Ta có ω = 20π → f = 10Hz → λ = v/f = 3 cm.
→ AB = 40 cm = 13λ + λ/3.
Những điểm dao động với biên độ 3 2 cm cách nút những khoảng λ/4.
→ Trên AB có số điểm dao động với biên độ 3 2 cm là: 13.4 + 2 = 54 điểm.