Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công lực cản cản trở chuyển động của viên đạn là
![]()
(Trọng lực P có phương vuông góc với chuyển động nên công của trọng lực bằng O)
Độ biến thiên động năng của vật là
![]()
![]()
Từ (1) và (2) theo định lý biến thiên động năng ta được:
![]()
Độ lớn lực cản trung bình của bức tường lên viên đạn bằng: Fc = 105000N

Chọn C.
Các lực tác dụng vào vật gồm:
+ Lực cản của tường
+ Trọng lực P ⇀
Công lực cản cản trở chuyển động của viên đạn là
A = F.s. cos α = F c .0,04.cos( 180 o ) (1)
(Trọng lực P ⇀ có phương vuông góc với chuyển động nên công của trọng lực bằng O)
Độ biến thiên động năng của vật là
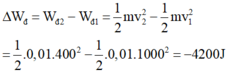
Từ (1) và (2) theo định lý biến thiên động năng ta được: F c
= -4200 ⇔ F c = 105000N
Độ lớn lực cản trung bình của bức tường lên viên đạn bằng: F c = 105000N.

Tóm đề:
m = 10 g
v0 = 600 m/s
t = \(\dfrac{1}{1000}\) s
v = 200 m/s
Giải
Theo định luật II Newton ta có \(m.a=F\Rightarrow m.\dfrac{v-v_0}{t}=F\)
\(\Rightarrow F=10.\dfrac{200-600}{\dfrac{1}{1000}}=-4.10^6\left(N\right)\)

Bài 1 :
P1 =m1g => m1 = 1(kg)
P2 = m2g => m2 =1,5(kg)
Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng : \(p_0=\left(m_1+m_2\right)v_0\)
Theo đl bảo toàn động lượng : \(p=p_0\Leftrightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v_0\)
=> \(v_1=\frac{\left(m_1+m_2\right)v_0-m_2v_2}{m_1}=\frac{\left(1+1,5\right).10-1,5.25}{1}=-12,5\left(m/s\right)\)
=> vận tốc v1 của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Bài2;
Vận tốc mảnh nhỏ trước khi nổ là :
v02=\(v_1^2=2gh\)
=> v1 = \(\sqrt{v_0^2-2gh}=\sqrt{100^2-2.10.125}=50\sqrt{3}\left(m/s\right)\)
Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
p = mv = 5.50 =250(kg.m/s)
\(\left\{{}\begin{matrix}p_1=m_1v_1=2.50\sqrt{3}=100\sqrt{3}\left(kg.m/s\right)\\p_2=m_2v_2=3.v_2\left(kg.m/s\right)\end{matrix}\right.\)
+ Vì \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\rightarrow\overrightarrow{p_1}\perp\overrightarrow{p_2}\)
=> p2 = \(\sqrt{p_1^2+p^2}=\sqrt{\left(100\sqrt{3}\right)^2+250^2}=50\sqrt{37}\left(kg.m/s\right)\)
=> v2= \(\frac{p_2}{m_2}=\frac{50\sqrt{37}}{3}\approx101,4m/s+sin\alpha=\frac{p_1}{p_2}=\frac{100\sqrt{3}}{50\sqrt{3}}\)
=> \(\alpha=34,72^o\)

0
Bình chọn giảm
Xét hệ là viên đạn. VÌ thời gan nổ là rất ngắn và trong thời gian nổ, nội lực rất lớn so với ngoại lực (trọng lực của đạn) nên hệ có thể coi là kín. Theo định luật bảo toàn động lượng ta có:
p⃗ =p1→+p2→⇔mv⃗ =m1v1→+m2v2→p→=p1→+p2→⇔mv→=m1v1→+m2v2→
Các vecto vận tốc như hình bên.
Về độ lớn ta có:
p=mv=200.2=400kg.m/sp=mv=200.2=400kg.m/s
p1=m1v1=1,5.200=300kg.m/sp1=m1v1=1,5.200=300kg.m/s
p2=p2+p21−−−−−−√=4002+3002−−−−−−−−−−√=500kg.m/sp2=p2+p12=4002+3002=500kg.m/s
Khối lượng mảnh thứ hai: m2=m−m1=0,5kgm2=m−m1=0,5kg
Vận tốc của mảnh thứ hai v2=p2m2=5000,5=1000m/sv2=p2m2=5000,5=1000m/s. Vận tốc v2→v2→ hợp với phương ngang một góc αα. Với tanα=p1p=34⇒α=370

Chọn chiều dương là chiều chuyển động của viên đạn
Độ biến thiên động lượng của viên đạn là
Δ p = m . v 2 − m . v 1 = 0 , 02 ( 200 − 600 ) = − 8 ( k g . m / s )
Áp dụng công thức
Δ p = m . v 2 − m . v 1 = 0 , 02 ( 200 − 600 ) = − 8 ( k g . m / s )

+ Chọn chiều dương là chiều chuyển động của viên đạn
+ Độ biến thiên động lượng của viên đạn là:
Δ p = m . v 2 − m . v 1 = 0 , 02 200 − 600 = − 8 k g . m / s
Áp dụng công thức:
Δ p = F . Δ t ⇒ F = Δ p Δ t = − 8 10 − 3 = - 8000 N
Chọn đáp án B

Đáp án B

Công lực cản cản trở chuyển động của viên đạn là
![]()
(Trọng lực P có phương vuông góc với chuyển động nên công của trọng lực bằng O)
Theo định lý biến thiên động năng ta được:
![]()
<=> Fc = 4500N
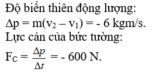
Chọn C.
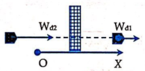
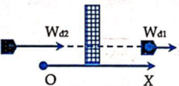
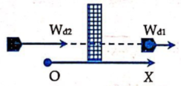
Các lực tác dụng vào vật gồm:
+ Lực cản của tường F C →
+ Trọng lực P →
Công lực cản cản trở chuyển động của viên đạn là
(Trọng lực có phương vuông góc với chuyển động nên công của trọng lực bằng O)
Độ biến thiên động năng của vật là
Từ (1) và (2) theo định lý biến thiên động năng ta được:
Độ lớn lực cản trung bình của bức tường lên viên đạn bằng: Fc = 105000N.