Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Chọn ngẫu nhiên 2 người có Ω = C 10 2 cách
Gọi A là biến cố: 2 người được chọn đều là nữ
Ta có Ω A = C 3 2 Do đó sác xuất cần tìm là P A = C 3 2 C 10 2 = 1 15

\(x^{15}-\left(7+1\right)x^{14}+\left(7+1\right)x^{13}....+\left(7+1\right)x-5\)
\(=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}....+\left(x+1\right)x-5\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}....-x^3-x^2+x^2+x-5\)
\(=x-5=7-5=2\)

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

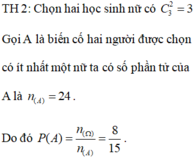



Chọn B.
Phương pháp
Tính xác suất theo định nghĩa P A = n A n Ω với n(A) là số phần tử của biến cố A, n Ω là số phấn tử
của không gian mẫu.
Cách giải:
Số phần tử của không gian mẫu n Ω = C 20 2
Gọi A là biến cố “Hai người được chọn có it nhất một nữ” thì A là biến cố hai người được chọn không có nữ nào, tức là ta chọn 2 người trong số 7 nam.
Khi đó n A = C 7 2 ⇒ n A = C 10 2 - C 7 2
Xác suất để hai người được chọn có it nhất một nữ là P = C 10 2 - C 7 2 C 10 2 = 8 15