Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/ \(y=3x+2\)
b/ \(y=-\frac{1}{4}x+1\)
c/ \(y=\frac{1}{6}x+\frac{3}{2}\)
d/ \(y=-32x-48\)
a/
\(0\le sin^2x\le1\Rightarrow-2\le f\left(x\right)\le1\)
\(f\left(x\right)_{min}=-2\) khi \(sin^2x=1\)
\(f\left(x\right)_{max}=1\) khi \(sin^2x=1\)
b/
\(g\left(x\right)=1-cos^2x+3cosx-2=-cos^2x+3cosx-1\)
\(=-cos^2x+3cosx-2+1=\left(cosx-1\right)\left(2-cosx\right)+1\)
Do \(-1\le cosx\le1\Rightarrow\left\{{}\begin{matrix}cosx-1\le0\\2-cosx>0\end{matrix}\right.\)
\(\Rightarrow\left(cosx-1\right)\left(2-cosx\right)\le0\Rightarrow g\left(x\right)\le1\)
\(g\left(x\right)_{max}=1\) khi \(cosx=1\)
\(g\left(x\right)=-cos^2x+3cosx+4-5=\left(cosx+1\right)\left(4-cosx\right)-5\)
\(\left(cosx+1\right)\left(4-cosx\right)\ge0\Rightarrow g\left(x\right)\ge-5\)
\(g\left(x\right)_{min}=-5\) khi \(cosx=-1\)
Tìm đạo hàm y' với y=\(\sqrt{X+\sqrt{1+x^2}}\). Mong mn giải chi tiết xíu để em có thể hiểu rõ hơn ạ
Lời giải:
Em không rõ ở phần tìm đạo hàm theo định nghĩa (lim) hay tìm đạo hàm dựa theo công thức
Thông thường lớp 11 thì thường áp dụng luôn công thức
Áp dụng công thức: \((u^{\alpha})'=\alpha.u'.u^{\alpha-1}\) thì:
\(y=(x+\sqrt{1+x^2})^{\frac{1}{2}}\)
\(\Rightarrow y'=\frac{1}{2}(x+\sqrt{x^2+1})'(x+\sqrt{x^2+1})^{\frac{1}{2}-1}\)
\(=\frac{(x+\sqrt{x^2+1})'}{2\sqrt{x+\sqrt{x^2+1}}}(*)\)
\((x+\sqrt{x^2+1})'=x'+(\sqrt{x^2+1})'=1+((x^2+1)^{\frac{1}{2}})'\)
\(=1+\frac{1}{2}(x^2+1)'(x^2+1)^{\frac{1}{2}-1}\)
\(=1+\frac{1}{2}.2x.\frac{1}{\sqrt{x^2+1}}=1+\frac{x}{\sqrt{x^2+1}}(**)\)
Từ \((*);(**)\Rightarrow y'=\frac{x+\sqrt{x^2+1}}{\sqrt{x^2+1}.2\sqrt{x+\sqrt{x^2+1}}}=\frac{1}{2}\sqrt{\frac{x+\sqrt{x^2+1}}{x^2+1}}\)
ta có : \(y'=\left(\sqrt{x+\sqrt{1+x^2}}\right)'=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(x+\sqrt{1+x^2}\right)'\)
\(=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(1+\dfrac{1}{2\sqrt{1+x^2}}\left(1+x^2\right)'\right)\) \(=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(1+\dfrac{2x}{2\sqrt{1+x^2}}\right)\) \(=\dfrac{1}{2\sqrt{x+\sqrt{1+x^2}}}\left(\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}\right)=\dfrac{1}{2}\sqrt{\dfrac{x+\sqrt{1+x^2}}{1+x^2}}\)
\(a=\lim\limits_{x\rightarrow1^+}\frac{\sqrt{x-1}+\sqrt{x}-1}{\sqrt{\left(x-1\right)\left(x+1\right)}}=\lim\limits_{x\rightarrow1^+}\left(\frac{1}{\sqrt{x+1}}+\frac{x-1}{\left(\sqrt{x}+1\right)\sqrt{\left(x-1\right)\left(x+1\right)}}\right)\)
\(=\lim\limits_{x\rightarrow1^+}\left(\frac{1}{\sqrt{x+1}}+\frac{\sqrt{x-1}}{\left(\sqrt{x}+1\right)\sqrt{x+1}}\right)=\frac{1}{\sqrt{2}}+0=\frac{1}{\sqrt{2}}\)
\(b=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x^{n-1}+x^{n-2}+...+x+1\right)}{\left(x-1\right)\left(x^{m-1}+x^{m-2}+...+x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x^{n-1}+x^{n-2}+...+1}{x^{m-1}+x^{m-2}+...+1}=\frac{n}{m}\)
\(c=\lim\limits_{x\rightarrow1}\frac{x-1+x^2-1+...+x^n-1}{x-1}=\lim\limits_{x\rightarrow1}\frac{x-1}{x-1}+\lim\limits_{\rightarrow1}\frac{x^2-1}{x-1}+...+\lim\limits_{x\rightarrow1}\frac{x^n-1}{x-1}\)
Áp dụng kết quả câu b ta được:
\(c=\frac{1}{1}+\frac{2}{1}+...+\frac{n}{1}=1+2+..+n=\frac{n\left(n+1\right)}{2}\)
1/
pt<=>tan(3x+2)=tan\(\dfrac{\Pi}{3}\)
<=>x=\(\dfrac{\Pi}{9}\)-\(\dfrac{2}{3}\)+\(\dfrac{k\Pi}{3}\)(k thuộc Z) (*)
mà x\(\in\)(\(-\dfrac{\Pi}{2}\);\(\dfrac{\Pi}{2}\))
<=>\(-\dfrac{\Pi}{2}\)<\(\dfrac{\Pi}{9}\)-\(\dfrac{2}{3}\)+\(\dfrac{k\Pi}{3}\)<\(\dfrac{\Pi}{2}\)(bạn giải bất pt với nghiệm là ''k'' nha)
<=>-1,1296....<k<1,803....
Mà k thuộc Z =>k={-1;01}
Thay các giá trị của k vào (*) ta được:
\(\left[{}\begin{matrix}x=-\dfrac{2\Pi}{9}-\dfrac{2}{3}\\x=\dfrac{\Pi}{9}-\dfrac{2}{3}\\x=\dfrac{4\Pi}{9}-\dfrac{2}{3}\end{matrix}\right.\)
Vậy.............
2/ Là tương tự cho quen nha!
Đáp án D
Đặt x, y, h lần lượt là chiều dài, chiều rộng và chiều cao mỗi phòng.
Theo giả thiết, ta có x.3y = 1152 → y = 384 x
Để tiết kiệm chi phí nhất khi diện tích toàn phần nhỏ nhất.
Ta có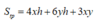
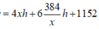
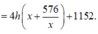
Vì h không đổi nên S t p nhỏ nhất khi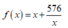
(với x > 0) nhỏ nhất.
Khảo sát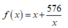
với x > 0 ta được f(x) nhỏ nhất khi x = 24 => y = 16