Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0
Gọi A' và d' theo thứ tự là ảnh của A và d qua phép biến hình trên
a) A' = (-1+2; 2+1) = (1;3), d // d', nên d có phương trình : 3x +y + C = 0. Vì A thuộc d, nên A' thuộc d', do đó 3.1 +3 + C = 0. Suy ra C=-6. Do đó phương trình của d' là 3x+y-6=0
b) A (-1;2) và B(0;-1) thuộc d. Ảnh của A và B qua phép đối xứng qua trục Oy tương ứng là A'(1;2) và B'(0;-1). Vậy d' là đường thẳng A'B' có phương trình :
=
hay 3x - y - 1 =0
c) A'=( 1;-2) , d' có phương trình 3x + y -1 =0
d) Qua phép quay tâm O góc , A biến thành A'( -2; -1), B biến thành B'(1;0). Vậy d' là đường thẳng A'B' có phương trình
=
hay x - 3y + 1 = 0

Lời giải:
Ta có: \(y=\frac{x+2}{2x+3}\Rightarrow y'=\frac{-1}{(2x+3)^2}\)
Gọi tiếp điểm có hoành độ là $a$. Khi đó pt tiếp tuyến của $(C)$ tại tiếp điểm là:
d: \(y=f'(a)(x-a)+f(a)=\frac{-1}{(2a+3)^2}(x-a)+\frac{a+2}{2a+3}(*)\)
Từ đây ta suy ra :
\(d\cap Ox=A(2a^2+8a+6,0)\)
\(d\cap Oy=B(0, \frac{2a^2+8a+6}{(2a+3)^2})\)
Vì tam giác $OAB$ cân tại $O$ nên:
\(OA=OB\Leftrightarrow |2a^2+8a+6|=|\frac{2a^2+8a+6}{(2a+3)^2}|\)
\(\Leftrightarrow |2a^2+8a+6|\left(1-\frac{1}{(2a+3)^2}\right)=0\)
Hiển nhiên $|2a^2+8a+6|\neq 0$ do $A$ khác $O$
\(\Rightarrow 1-\frac{1}{(2a+3)^2}=0\Rightarrow (2a+3)^2=1\)
\(\Rightarrow 2a+3=\pm 1\Rightarrow a=-2; a=-1\)
Thay vào $(*)$ suy ra PTTT là:
\(\left[\begin{matrix}
y=-x\\
y=-x-2\end{matrix}\right.\)

\(y'=\frac{-1}{\left(x-1\right)^2}\), gọi \(M\left(a;\frac{1}{a-1}\right)\)
Phương trình tiếp tuyến d qua M:
\(y=\frac{-1}{\left(a-1\right)^2}\left(x-a\right)+\frac{1}{a-1}\)
Gọi giao điểm của d với Ox và Oy lần lượt là A và B \(\Rightarrow\left\{{}\begin{matrix}A\left(2a-1;0\right)\\B\left(0;\frac{2a}{\left(a-1\right)^2}\right)\end{matrix}\right.\)
Do \(S_{OAB}=2\Rightarrow\frac{1}{2}OA.OB=2\Rightarrow OA.OB=4\)
\(\Rightarrow\left|\left(2a-1\right)\frac{2a}{\left(a-1\right)^2}\right|=4\Rightarrow\left\{{}\begin{matrix}\frac{2a\left(2a-1\right)}{\left(a-1\right)^2}=4\\\frac{2a\left(2a-1\right)}{\left(a-1\right)^2}=-4\end{matrix}\right.\) \(\Rightarrow a=\frac{2}{3}\)
\(\Rightarrow M\left(\frac{2}{3};-3\right)\)


Chọn C
Mỗi bước người này có 2 lựa chọn sang trái hoặc phải nên số phần tử không gian mẫu là 2 10 .
Để sau đúng 10 bước người này quay lại đúng gốc tọa độ O thì người này phải sang trái 5 lần và sang phải 5 lần, do đó số cách bước trong 10 bước này là C 10 5 .
Xác suất cần tính bằng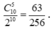 .
.