Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ nở dài của dây tải điện đó khi nhiệt độ tăng lên đến 50 độ C là:
\(\Delta l=l-l_0=\alpha.l_0.\Delta t=11,5.10^{-6}.30.1800=0,621\left(m\right)\)Vậy: ...

Đáp án: A
Độ nở dài của dây tải điện:
Dl = al0Dto = 0,414 m = 41,4 cm.

t1 = 20o C, l1 = 1800 m
t2 = 50o C
α = 11,5.10-6 (k-1)
Δl = ?
Áp dụng công thức :
Δl = αl1Δt
Δl = 11,5.10-6.1800.(50 - 20) = 0,621 m
Vậy độ nở dài của dây tải điện là Δl = 0,621 (m)

\(\Delta l=\alpha l_0\Delta t=11,5.10^{-6}.1800.\left(50-20\right)=0,612m\)

Độ tăng nhiệt độ:
\(\Delta t=t_2-t_1=50-20=30^oC\)
Độ nở dài của dây dẫn:
\(l=l_0\left(1+\alpha\Delta t\right)=1500\cdot\left(1+11,5\cdot10^{-6}\cdot30\right)=1500,5175m\)

a/ Chiều dài của thanh: \(l=l_0(1+\alpha.\Delta t)\)
Thanh nhôm: \(l=50.[1+24.10^{-6}.(170-20)]=50,18cm\)
Thanh thép: \(l=50,12.[1+12.10^{-6}.(170-20)]=50,21cm\)
b/ Giả sử ở nhiệt độ t, hai thanh có cùng chiều dài
\(\Rightarrow 50.[1+24.10^{-6}.(t-20)]=50,12.[1+12.10^{-6}.(t-20)]\)
Bạn giải phương trình trên rồi tìm t nhé ![]()

Chọn đáp án B
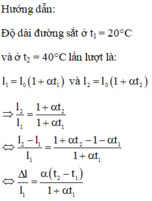
Vì α t 1 << 1 nên khi nhiệt độ tăng từ t 1 = 20 ° C đến t 2 = 40 ° C thì đoạn đường sắt này sẽ dài thêm một đoạn đường gần đúng bằng
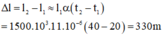

* Cách 1 :
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : △l = l0a . △t
→ Độ biến dạng thiên nhiệt độ △t :
△t = \(\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-8}}=0,03.10^3=30^oC\)
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = △t + t = 15oC + 30oC = 45oC
Đáp số 450C
* Cách 2 :
Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o
Độ nở dài của dây tải điện: Dl = a l 0 Dt = 0,414 m = 41,4 cm.