Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Khi giọt nước rơi khỏi miệng ống thì trọng lượng P của nó bằng lực căng bề mặt F C tác dụng lên giọt nước tại miệng ống:
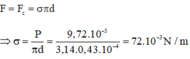

Độ nở dài của dây tải điện: Dl = a l 0 Dt = 0,414 m = 41,4 cm.

Đáp án: A
Độ nở dài của dây tải điện:
Dl = al0Dto = 0,414 m = 41,4 cm.

t1 = 20o C, l1 = 1800 m
t2 = 50o C
α = 11,5.10-6 (k-1)
Δl = ?
Áp dụng công thức :
Δl = αl1Δt
Δl = 11,5.10-6.1800.(50 - 20) = 0,621 m
Vậy độ nở dài của dây tải điện là Δl = 0,621 (m)

\(\Delta l=\alpha l_0\Delta t=11,5.10^{-6}.1800.\left(50-20\right)=0,612m\)

B3: to = 20C
\(\Delta l=l_o\alpha\left(50-20\right)=0,0033m\)
=> phải để hở 1 khe lớn hơn hoặc = 0,0033m
B1: a, \(\Delta l=l_o\alpha\left(40-20\right)=0,00033m\)
b, \(l=\Delta l+l_o=1,50033m\)
B5: Ta co: \(V=V_o\left[1+3\alpha\left(t-t_o\right)\right]\)
=> \(\frac{m}{D}=\frac{m}{D_o}\left[1+3\alpha\left(500-0\right)\right]\)
=> D \(\approx6885,4\)
B2: \(l-l_o=l_o\alpha\left(t-0\right)\)
=> \(l_o\alpha\left(t-0\right)=0,0008\)
=> \(t\approx72,7^oC\)

* Cách 1 :
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : △l = l0a . △t
→ Độ biến dạng thiên nhiệt độ △t :
△t = \(\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-8}}=0,03.10^3=30^oC\)
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = △t + t = 15oC + 30oC = 45oC
Đáp số 450C
* Cách 2 :
Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o

Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o.
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : \(\triangle\)l = l0a . \(\triangle\)t
→ Độ biến dạng thiên nhiệt độ \(\triangle\)t :
\(\triangle t=\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-6}}=0,03.10^3=30\) độ C
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = \(\triangle\)t + t = 15 độ C + 30 độ C = 45 độ C
Đáp số 45 độ C

Chọn đáp án B
Vì α t 1 << 1 nên khi nhiệt độ tăng từ t 1 = 20 ° C đến t 2 = 40 ° C thì đoạn đường sắt này sẽ dài thêm một đoạn đường gần đúng bằng