Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)khi cố định đầu dưới đầu còn lại đặt vật có m=0,4kg lên
\(F_{đh}=P\Rightarrow k.\left(l_0-l\right)=m.g\)
\(\Rightarrow\)l0=0,27m\(\Rightarrow\Delta l=l_0-l=0,05m\)
b)đặt thêm vật m1=0,2kg, lúc này khối lượng vật đặt lên lò xo là m'=0,6kg
chiều dài lò xo lúc này
k.(l0-l1)=m'.g\(\Rightarrow\)l1=0,2625m

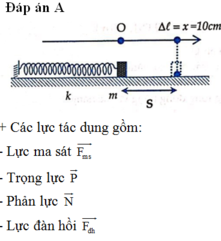
+ Khi tính công ta chú ý không tính công của lực đàn hồi. Do vậy ta có:
![]()
![]()
Cơ năng của vật lúc đầu (buông nhẹ) là
![]()
![]()
Cơ năng của vật sau khi đi quãng đường 10cm là
![]()
Do vật chịu tác dụng thêm lực ma sát cơ năng của vật sẽ biến đổi. Công của các lực cản bằng độ biến thiên cơ năng của vật:
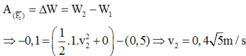

Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...

Độ dãn tối đa \(\Delta l_o=\frac{mg}{k}\)
Vận tốc lớn nhất \(v_{max}=\omega A=\sqrt{\frac{k}{m}}\frac{mg}{k}=g\sqrt{\frac{m}{k}}\)

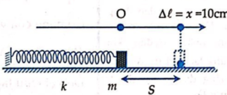

+ Khi tính công ta chú ý rằng không tính công của lực đàn hồi. Do vậy ta có:
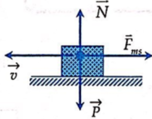
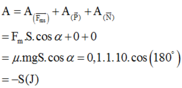
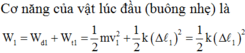
Cơ năng của vật sau khi tắt hẳn (dừng lại) là
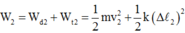
![]()
Do vật chịu tác dụng thêm lực ma sát cơ năng của vật sẽ biến đổi. Công của các lực cản bằng độ biến thiên cơ năng của vật:
![]()
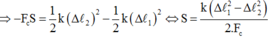
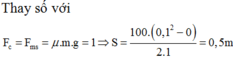

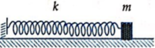
Kéo quả nặng đến vị trí lò xo giãn 5 cm → A = 5 cm.
Tần số góc ω = Căn (k/m) = Căn (25/0.25) = 10 rad/s.
Tại thời điểm t = 0 vật đi qua vị trí cân bằng lần đầu tiên → φ = -π/2 rad.
→ phương trình dao động của quả nặng là x = 5cos(10t – π/2) cm.

Bài 1:
\(\alpha= 0\) \(\Rightarrow F = F_1+F_2 = 16+12=28N\)
\(\alpha = 30^0\)\(\Rightarrow F^2=16^2+12^2+2.16.12.\cos30^0=...\Rightarrow F\)
Các trường hợp khác bạn tự tính nhé.
Bài 2:
Ta có: \(F_1=k.\Delta \ell_1=k.(0,24-0,12)=0,12.k=5\) (1)
\(F_1=k.\Delta \ell_2=k.(\ell-0,12)=10\) (2)
Lấy (2) chia (1) vế với vế: \(\dfrac{\ell-0,12}{0,12}=2\)
\(\Rightarrow \ell = 0,36m = 36cm\)
Bài 3:
Áp lực lên sàn: \(N=P=mg\)
Áp dụng định luật II Niu tơn ta có: \(F=m.a\Rightarrow -F_{ms}=ma\)
\(\Rightarrow a = \dfrac{-F_{ms}}{m}= \dfrac{-\mu.N}{m}== \dfrac{-\mu.mg}{m}=-\mu .g =- 0,1.10=-1\)(m/s2)
Quãng đường vật đi được đến khi dừng lại là \(S\)
Áp dụng công thức độc lập: \(v^2-v_0^2=2.a.S\)
\(\Rightarrow 0^2-10^2=2.1.S\Rightarrow S = 50m\)

Giải :
\(\bigtriangleup\text{l}_1=\text{l}_1-\text{l}_0=30,5-20=0,5\left(\text{cm}\right)\)
\(\text{m}=\text{m}_1+\text{m}_2=20+80=100\left(\text{g}\right)=5\text{m}_1\)
\(\Rightarrow \bigtriangleup\text{l}_2=5\bigtriangleup\text{l}_1=5\cdot0,5=2,5\left(\text{cm}\right)\)
\(\Rightarrow\text{ l}_2=\text{l}_0+\bigtriangleup\text{l}_2=30+2,5=32,5\left(\text{cm}\right)\)
 10
10
Đáp án C
Cơ năng của vật lúc đầu (buông nhẹ) là
Cơ năng của vật lúc sau (trạng thái có độ biến dạng ∆ l 1 = 1cm)
Do vật chịu tác dụng thêm lực ma sát ca năng của vật sẽ biến đổi. Công của các lực cản bằng độ biến thiên cơ năng của vật: