Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D.
Theo bài:
W d 1 = 2 W t 1 ⇒ 1 3 = W t W = x A 2 = 3 A 2 ⇒ A 2 = 27
Lúc li độ bằng 1cm thì
W t 2 W = 1 A 2 = 1 27 ⇒ W d 2 = 26 W t 2
Vậy so với thế năng đàn hồi của lò xo thì động năng của vật lớn gấp 2 lần

Đáp án D
Theo bài:
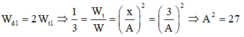
Lúc li độ bằng 1cm thì
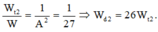
Vậy so với thế năng đàn hồi của lò xo thì động năng của vật lớn gấp 2 lần.

Đáp án A.
Lời giải chi tiết:
Từ giả thiết ta có giữa hai lần động năng bằng thế năng thì
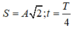
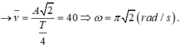
Khi động năng của chất điểm bằng 1/3 lần thế năng thì
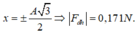

Gọi A là biên độ giao động ta có : kA = 10 N; kA2/2 = 1J => A = 0,2 m = 20 cm
Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp Q chịu tác dụng lực kéo của lò xo có độ lớn \(5\sqrt{3}\)
=> Chu kì giao động của vật T = 0,6s
Quãng đường ngắn nhất đi được là trong 0,4s = \(\frac{2T}{3}\) là s = 3A = 60 cm
Vậy B đúng

Đáp án B
Phương pháp: Áp dụng công thức tính lực độ lớn lực đàn hồi cực đại của con lắc lò xo dao động điều hoà theo phương thẳng đứng.
Cách giải:
Vật ở vị trí cân bằng thì lò xo dãn một đoạn ∆l.
Ta có:
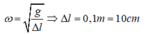
Khi động năng bằng thế năng thì:
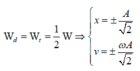
Khi đó:
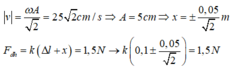
Vì k < 20N/m nên lấy k = 11N/m
Độ lớn cực đại của lực đàn hồi:
![]()

mình cho bạn cái này thử vào áp dụng nhé:
Wđ = n Wt => \(x =\pm {A \over \sqrt{n+1}}\)
\(W_đ=W_t\)
\(\Rightarrow W = W_đ+W_t = 2W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=2.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{A}{\sqrt 2}=\pm2\sqrt 2\) (cm)

Nhớ biểu thức sau, rất hữu ích khi thi trắc nghiệm
\(W_d=n.W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{n+1}}\)
\(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
\(\Rightarrow F_{dh}=k.\Delta l=k.\dfrac{A}{2}=\dfrac{1}{2}kA\left(N\right)\)
\(F_{dh\left(max\right)}=kA\left(N\right)\)
\(\Rightarrow\dfrac{F_{dh}}{F_{dh\left(max\right)}}=\dfrac{\dfrac{1}{2}kA}{kA}=\dfrac{1}{2}\)

Chọn A