Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Lời giải chi tiết:
Từ giả thiết ta có giữa hai lần động năng bằng thế năng thì
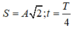
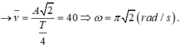
Khi động năng của chất điểm bằng 1/3 lần thế năng thì
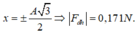

Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)

Đáp án C
Độ biến dạng của lò xo tại vị trí cân bằng
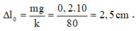
Kéo vật đến vị trí lò xo giãn 7,5 cm rồi thả nhẹ → vật sẽ dao động với biên độ A=5cm.
→ Lực đàn hồi có độ lớn nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng.
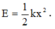
Thế năng của con lắc bằng tổng thế năng đàn hồi và thế năng hấp dẫn. Với gốc thế năng tại vị trí cân bằng thì .
→ Thế năng đàn hồi khi đó có độ lớn
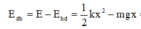
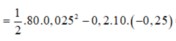
=-0,025J

Nhớ biểu thức sau, rất hữu ích khi thi trắc nghiệm
\(W_d=n.W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{n+1}}\)
\(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
\(\Rightarrow F_{dh}=k.\Delta l=k.\dfrac{A}{2}=\dfrac{1}{2}kA\left(N\right)\)
\(F_{dh\left(max\right)}=kA\left(N\right)\)
\(\Rightarrow\dfrac{F_{dh}}{F_{dh\left(max\right)}}=\dfrac{\dfrac{1}{2}kA}{kA}=\dfrac{1}{2}\)

Đáp án B
Phương pháp: Áp dụng công thức tính lực độ lớn lực đàn hồi cực đại của con lắc lò xo dao động điều hoà theo phương thẳng đứng.
Cách giải:
Vật ở vị trí cân bằng thì lò xo dãn một đoạn ∆l.
Ta có:
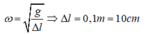
Khi động năng bằng thế năng thì:
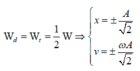
Khi đó:
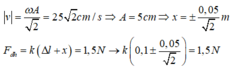
Vì k < 20N/m nên lấy k = 11N/m
Độ lớn cực đại của lực đàn hồi:
![]()




Đáp án A