Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động của con lắc đơn chịu tác dụng của lực điện trường
Cách giải:
+ Cường độ điện trường giữa hai bản kim loại E = U/d
+ Gia tốc trọng trường hiệu dụng:
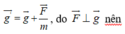
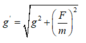
Mà
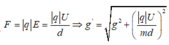
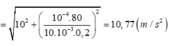
+ Chu kì dao động nhỏ của con lắc là:
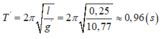
=> Chọn A

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động của con lắc đơn chịu tác dụng của lực điện trường
Cách giải:
+ Cường độ điện trường giữa hai bản kim loại E = U/d
+ Gia tốc trọng trường hiệu dụng:
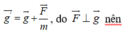
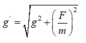
Mà
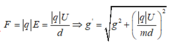
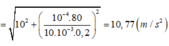
+ Chu kì dao động nhỏ của con lắc là:
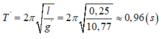
=> Chọn A

Theo giả thiết thì hai bản tụ đặt thẳng đứng trái dấu, nên ta có hình sau:
+ + + + + - - - - - α E P F T
Góc lệch ở VTCB: \(\tan\alpha=\frac{F}{P}=\frac{qE}{mg}=\frac{qU}{mgd}=\frac{10^{-5}.400}{0,01.10.0,1}=0,4\)
\(\Rightarrow\alpha=21,8^0\)

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)



 =2 7,1 cm/s
=2 7,1 cm/s
Cường độ điện trường giữa hai bản tụ điện
Đáp án C