Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động của con lắc đơn chịu tác dụng của lực điện trường
Cách giải:
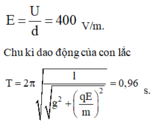
+ Cường độ điện trường giữa hai bản kim loại E = U/d
+ Gia tốc trọng trường hiệu dụng:
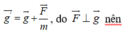
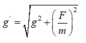
Mà
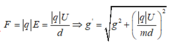
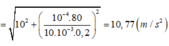
+ Chu kì dao động nhỏ của con lắc là:
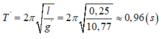
=> Chọn A

Theo giả thiết thì hai bản tụ đặt thẳng đứng trái dấu, nên ta có hình sau:
+ + + + + - - - - - α E P F T
Góc lệch ở VTCB: \(\tan\alpha=\frac{F}{P}=\frac{qE}{mg}=\frac{qU}{mgd}=\frac{10^{-5}.400}{0,01.10.0,1}=0,4\)
\(\Rightarrow\alpha=21,8^0\)

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Ta có: \(\omega=2\pi f=5\pi\) ; A = 4cm
\(\omega=\sqrt{\frac{K}{m}}=\sqrt{\frac{K}{0,1}}\Rightarrow K=25\)
\(\Delta l_o=\frac{mg}{k}=\frac{0,1.10}{25}=4cm\)
Áp dụng CT: \(F_{đh}max=K\left(\Delta l_o+A\right)\) và \(F_{đh}min=k\left(\Delta l_o-A\right)\)
Suy ra, Fmax = 2 N và Fmin = 0 N
Theo mình là đáp án khác.


Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động của con lắc đơn chịu tác dụng của lực điện trường
Cách giải:
+ Cường độ điện trường giữa hai bản kim loại E = U/d
+ Gia tốc trọng trường hiệu dụng:
Mà
+ Chu kì dao động nhỏ của con lắc là:
=> Chọn A