
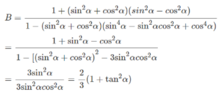
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

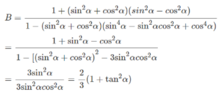

a) Lấy (1)+(2)+(3) là tìm được z rồi thế z vào tìm x, y
b) Lấy (1) + (2) - (3) là tìm được y
\(a)\hept{\begin{cases}x-2y+z=12\\2x-y+3z=18\\-3x+3y+2z=-9\end{cases}\Leftrightarrow\hept{\begin{cases}x-2y+z=12\\3y+z=-6\\6z=21\end{cases}}}\)
\(\text{Đáp số: }(x;y;z)=(\frac{16}{3};-\frac{19}{6};\frac{7}{2})\)
\(b)\hept{\begin{cases}x+y+z=7\\3x-2y+2z=5\\4x-y+3z=10\end{cases}\Leftrightarrow}\hept{\begin{cases}x+y+z=7\\-5y-z=16\\0y+0z=-2\end{cases}}\)
\(\text{ Hệ phương trình vô nghiệm.}\)



Gọi độ dài mỗi cạnh của tam giác lần lượt là x;y;z
Theo bài ra ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) và x+y+z=72
theo tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{72}{12}=6\)
=> x=18
y=24
z=30
Bài 21:
Gọi độ dài 3 cạnh của tam giác đó là: a, b, c ( a, b, c > 0 )
Theo đề bài, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a + b + c = 72
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{72}{12}=6\)
Do đó:
\(\frac{a}{3}=6=>a=6\cdot3=18\)
\(\frac{b}{4}=6=>b=6\cdot4=24\)
\(\frac{c}{5}=6=>c=6\cdot5=30\)
Vậy độ dài 3 cạnh của tam giác đó theo thứ tự là: 18; 24; 30 ( cm ) thỏa mãn yêu cầu đề bài
Bài 22:
Gọi số học sinh 3 lớp 7A, 7B, 7C theo thứ tự là: a, b, c ( a, b, c thuộc N* )
Theo đề bài, ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\) và c - a = 16
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{c-a}{6-4}=\frac{16}{2}=8\)
Do đó:
\(\frac{a}{4}=8=>a=8\cdot4=32\)
\(\frac{b}{5}=8=>b=8\cdot5=40\)
\(\frac{c}{6}=8=>c=8\cdot6=48\)
Vậy số học sinh 3 lớp 7A, 7B, 7C theo thứ tự là: 32; 40; 48 ( học sinh ) thỏa mãn yêu cầu đề bài




\(A=tan18^otan288+sin32^osin148^o-sin302^osin122^o\)
\(=tan18^o.tan\left(-72^o\right)+sin32^o.sin32^o+sin58^o.sin58^o\)
\(=-tan18^o.cot18^o+sin^232^o+sin^258^o\)
\(=-1+sin^232^o+cos^232^2=-1+1=0\).
b) \(B=\dfrac{1+sin^4\alpha-cos^4\alpha}{1-sin^6\alpha-cos^6\alpha}\)
\(=\dfrac{1+\left(sin^2\alpha+cos^2\alpha\right)\left(sin^2\alpha-cos^2\alpha\right)}{1-\left(sin^6\alpha+cos^6\alpha\right)}\)
\(=\dfrac{1+sin^2\alpha-cos^2\alpha}{1-\left(sin^2\alpha+cos^2\alpha\right)\left(sin^2\alpha-sin\alpha cos\alpha+cos^2\alpha\right)}\)
\(=\dfrac{sin^2\alpha+1-cos^2\alpha}{1-\left(1-sin\alpha.cos\alpha\right)}\)
\(=\dfrac{sin^2\alpha+sin^2\alpha}{sin\alpha cos\alpha}\)
\(=\dfrac{2sin^2\alpha}{sin\alpha cos\alpha}=\dfrac{2sin\alpha}{cos\alpha}=2tan\alpha\).
