Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác vuông FGC có \(\widehat{C}=45^0\) nên là tam giác vuông cân. Do đó FG = GC


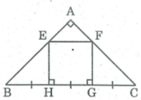
Vì ΔABC vuông cân tại A nên ∠ B = ∠ C = 45 0
Vì ΔBHE vuông tại H có ∠ B = 45 0 nên ΔBHE vuông cân tại H.
Suy ra HB = HE
Vì ΔCGF vuông tại G, có ∠ C = 45 0 nên ΔCGF vuông cân tại G
Suy ra GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);
Lại có ∠ (EHG) = 90 0 nên HEFG là hình chữ nhật.
Mà EH = HG (chứng minh trên).
Vậy HEFG là hình vuông.

1:
ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
EH\(\perp\)BC tại H
=>EH\(\perp\)HB tại H
=>ΔEHB vuông tại H
Xét ΔHEB vuông tại H có \(\widehat{HBE}=45^0\)
nên ΔHEB vuông cân tại H
FG\(\perp\)BC tại G
=>FG\(\perp\)GC tại G
=>ΔFGC vuông tại G
Xét ΔFCG vuông tại G có \(\widehat{GCF}=45^0\)
nên ΔFCG vuông cân tại G
2: EH\(\perp\)BC
FG\(\perp\)BC
Do đó: EH//FG
EH=HB
HB=HG=GC
GF=GC
Do đó; EH=HB=GH=CG=GF
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHFG là hình bình hành
Hình bình hành EHFG có \(\widehat{EHG}=90^0\)
nên EHFG là hình chữ nhật
Hình chữ nhật EHFG có GH=GF
nên EHFG là hình vuông

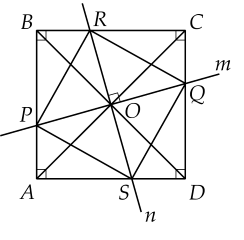
a) Do ABCD là hình vuôn nên:
\(AB=BC=CD=AD\)
Mà: \(\left\{{}\begin{matrix}AB=AM+MB\\BC=BN+NC\\CD=CP+PD\\AD=DQ+QA\end{matrix}\right.\)
Lại có: \(AM=BN=CP=DQ\)
\(\Rightarrow MB=NC=PD=QA\left(dpcm\right)\)
b) Xét \(\Delta QAM\) và \(\Delta NCP\) có:
\(\widehat{A}=\widehat{C}=90^o\left(gt\right)\)
\(AM=CP\left(gt\right)\)
\(QA=NC\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP\left(c.g.c\right)\)
c) Xét các tam giác: \(\Delta QAM,\Delta NCP,\Delta PDQ,\Delta MBN\) ta có:
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^o\left(gt\right)\)
\(AM=BN=CP=DQ\left(gt\right)\)
\(MB=NC=PD=QA\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP=\Delta PDQ=\Delta MBN\left(c.g.c\right)\)
\(\Rightarrow MQ=QP=PN=NM\) (các cạnh tương ứng)
\(\Rightarrow MNPQ\) là hình thoi (1)
Xét tam giác QAM ta có:
\(\widehat{QMA}+\widehat{AQM}=180^o-90^o=90^o\)
Mà: \(\Delta QAM=\Delta MBN\left(cmt\right)\)
\(\Rightarrow\widehat{BMN}=\widehat{AQM}\) (hai góc tương ứng)
\(\Rightarrow\widehat{BMN}+\widehat{QMA}=90^o\)
Lại có: \(\widehat{BMN}+\widehat{QMA}+\widehat{NMQ}=180^o\)
\(\Rightarrow\widehat{NMQ}=180^o-90^o=90^o\) (2)
Từ (1) và (2) ta có MNPQ là hình vuông
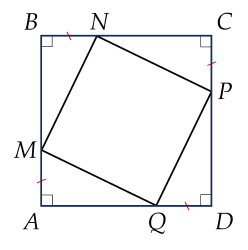
a) ����ABCD là hình vuông nên ��=��=��=��AB=BC=CD=DA
Mà ��=��=��=��AM=BN=CP=DQ.
Trừ theo vế ta được ��−��=��−��=��−��=��−��AB−AM=BC−BN=CD−CP=DA−DQ
Suy ra ��=��=��=��MB=NC=PD=QA
Xét tam giác QAM và tam giác NPC có:
góc A = góc C = 90 độ
AQ=NC(cmt)
AM=CP(gt)
=>Tam giác QAM= tam giác NPC(c.g.c)
c)=> NP = MQ ( hai cạnh tương ứng)
Chứng minh tương tự như phần b ta có: Tam giác QAM= tam giác PDQ và tam giác QAM= tam giác MBN
Khi đó: MQ=PQ, MN=MQ và góc AMQ= góc DQP
Mà góc AMQ+AQM=90 độ
=>góc DQP+ góc AQM= 90 độ
Do đó góc MQP = 90 độ
tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi
Lại có góc MQP = 90 độ nên là hình vuông
Vậy tứ giác MNPQ là hình vuông


a) Ta thấy ngay \(\Delta ABE=\Delta ACD\) (Hai cạnh góc vuông)
b) Do \(\Delta ABE=\Delta ACD\Rightarrow\widehat{ABE}=\widehat{ACD}\)
mà \(\widehat{ABE}=\widehat{MAC}\) (Cùng phụ với góc BEA)
\(\Rightarrow\widehat{MAC}=\widehat{MCA}\) hay tam giác MAC cân tại M.
c) Xét tam giác vuông ADC: \(\widehat{MCA}=\widehat{MAC}\Rightarrow\widehat{MDA}=\widehat{MAD}\Rightarrow MD=MA\)
Vậy thì DM = MA = MC hay M là trung điểm DC.
Xét tam giácAIC có M là trung điểm DC, MK // DI nên MK là đường trung bình tam giác DIC.
Suy ra K là trung điểm IC.
d) Xét tam giác DIC có IM và DK là hai trung tuyến nên G là trọng tâm tam giác.
Gọi N là giao điểm của CG với DE thì DN = NI.
Áp dụng định lý Talet ta có:
\(\frac{MF}{DN}=\frac{CF}{CN}=\frac{FK}{NI}\)
Mà DN = NI nên MF = FK.

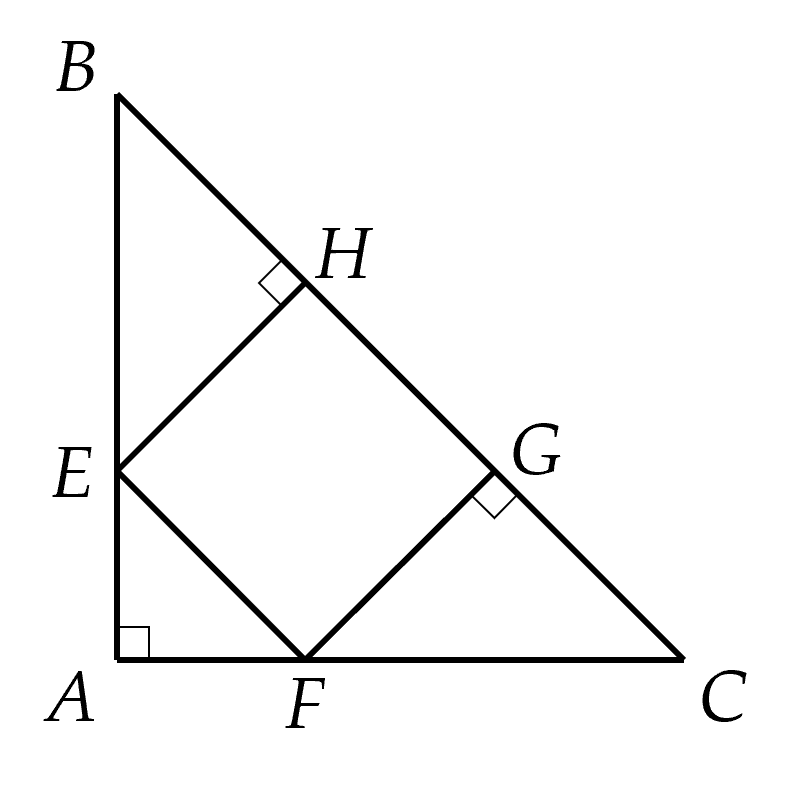
1. ta có AD = BC (gt)
mà DH = BF (gt)
=> AH =FC
xét ▲AHE và ▲FCG, có:
AE = CG (gt)
góc A = góc C (gt)
AH = FC (cmt)
=>▲AHE = ▲FCG (c.g.c)
=>HE = FG (2 cạnh t/ứ)
cmtt : HG = EF
Vậy EFGH là hbh (đpcm)

a) Δ��� Tam giác ABC vuông cân nên góc B= góc C = 45 độ
Tam giácBHE vuông tại H có góc BEH + góc B = 90 độ
Suy ra góc BEH = 90 độ - 45 độ = 45 độ nên góc B= góc BEH = 45 độ
Vậy tam giác BEH vuông tại H
b) Chứng minh tương tự như câu a ta được tam giác CFG vuông tại G nên GF=GC và HB=HE
Lại có BH=HG=GC suy ra EH=HG=GF và EH//FG ( cùng vuông góc với BC)
Tứ giác EFGH có EH//FG, EH=FG
=>tứ giác EFGH là hình bình hành
Xét hình bình hành có một góc vuông là góc H nên là hình chữ nhật
Mà hình chữ nhật có hai cạnh kề bằng nhau là EH=HG nên là hình vuông
Vậy EFGH là hình vuông
a) Δ���ΔABC vuông cân nên �^=�^=45∘.B=C=45∘.
Δ���ΔBHE vuông tại �H có ���^+�^=90∘BEH+B=90∘
Suy ra ���^=90∘−45∘=45∘BEH=90∘−45∘=45∘ nên �^=���^=45∘B=BEH=45∘.
Vậy Δ���ΔBEH vuông cân tại �.H.
b) Chứng minh tương tự câu a ta được Δ���ΔCFG vuông cân tại �G nên ��=��GF=GC và ��=��HB=HE
Mặt khác ��=��=��BH=HG=GC suy ra ��=��=��EH=HG=GF và ��EH // ��FG (cùng vuông góc với ��)BC)
Tứ giác ����EFGH có ��EH // ��,��=��FG,EH=FG nên là hình bình hành.
Hình bình hành ����EFGH có một góc vuông �^H nên là hình chữ nhật
Hình chữ nhật ����EFGH có hai cạnh kề bằng nhau ��=��EH=HG nên là hình vuông.