Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phần tử của không gian mẫu là: `n(Ω)=6`
A: "Số chấm xuất hiện nhỏ hơn ba"
`-> n(A)= 2`
`=> P(A)=(n(Ω))/(n(A))=2/6=1/3`
`=>` A.

Xác suất:
a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)
b. \(\dfrac{6}{36}=\dfrac{1}{6}\)
c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng
\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10
Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)

Rõ ràng \(\Omega=\left\{\left(i;j\right):1\le i,j\le6\right\}\)
Kí hiệu :
\(A_1:\) "Lần đầu xuất hiện mặt 1 chấm"
\(B_1:\) "Lần thứ hai xuất hiện mặt 1 chấm"
\(C:\) " Tổng số chấm là 6"
\(D:\) "Mặt 1 chấm xuất hiện ít nhất một lần"
a) Ta có \(C=\left\{\left(1,5\right),\left(5,1\right),\left(2,4\right),\left(4,2\right)\left(3,3\right)\right\},P\left(C\right)=\dfrac{5}{36}\)
b) Ta có \(A_1,B_1\) độc lập và \(D=A_1\cup B_1\) nên
\(P\left(D\right)=P\left(A_1\right)+P\left(B_1\right)-P\left(A_1B_1\right)\)
\(=\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{6}.\dfrac{1}{6}=\dfrac{11}{36}\)

Chọn B
Không gian mẫu là: ![]()
Gọi A là biến cố: “Mặt có số chấm chẵn xuất hiện”.
![]()
Xác suất để mặt có số chấm chẵn xuất hiện là:
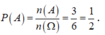

Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với ![]()
⇒ ![]()
⇒ ![]()
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
![]()
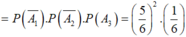

Chọn D
Theo đề bài b là số chấm của con súc sắc nên b ∈ {1;2;3;4;5;6}
Để phương trình
x
2
+ 2bx + 4 = 0 có nghiệm thì ![]()
Kết hợp b ∈ [1;6] suy ra b ∈ {2;3;4;5;6} Suy ra xác suất để phương trình
x 2 + 2bx + 4 = 0 có nghiệm là 5 6



Chọn C
Gọi A là biến cố “ Súc sắc xuất hiện mặt chẵn chấm”