Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho 2014=2013+1 thay vào ta có:\(B=x^{2013}-\left(2013+1\right)x^{2012}+\left(2013+1\right)x^{2011}-...-\left(2013+1\right)x^2+\left(2013+1\right)x-1\)
\(=x^{2013}-\left(x+1\right)x^{2012}+\left(x+1\right)x^{2011}-...-\left(x+1\right)x^2+\left(x+1\right)x-1\)
\(=x^{2013}-x^{2013}-x^{2012}+x^{2012}+x^{2011}-...-x^3-x^2+x^2+x-1\)
\(=x-1=2013-1=2012\)

Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
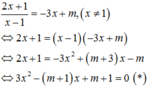
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
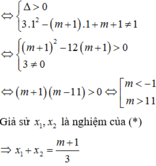


Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.

Đáp án A
Ta có 5 log c 6 = 6 log c 5 ⇔ 5 log c 6 + − 6 log c 5 = 0 . Mà
f − x = a ln 2017 x 2 + 1 − x − b x sin 2018 x + 2
a ln 2017 1 x 2 + 1 + x − b x sin 2018 x + 2 = − a ln 2017 x 2 + 1 + x − b x sin 2018 x + 2
⇒ f x + f − x = 4 ⇒ f − 6 log c 5 + f 5 log c 6 = 4 ⇒ f − 6 log c 5 = − 2

Đặt x = a - t nên dx = -dt. Ta có
I = - ∫ a 0 d t 1 + f a - t = ∫ 0 a d t 1 + 1 f t = ∫ 0 a f t 1 + f t d t
Suy ra 2I = I + I = ∫ 0 a d t = a. Vậy I = a 2
Đáp án B

Đặt t = 3 x > 0 . Bất phương trình đã cho trở thành
a t 2 + 9 a - 1 t + a - 1 > 0 ⇔ a > 9 t t 2 + 9 t + 1
Bất phương trình đã cho nghiệm đúng với mọi x khi và chỉ khi a > m a x t ∈ 0 ; + ∞ f t với f t = 9 t t 2 + 9 t + 1
Ta có f ' t = - 9 t 2 t 2 + 9 t + 1 2 < 0 ; ∀ t > 0 ⇒ f t là hàm nghịch biến trên 0 ; + ∞ .
Suy ra f(t) < f(0) = 1
Do đó 9 t t 2 + 9 t + 1 < 1 ; ∀ t > 0 nên các giá trị của a cần tìm là a ≥ 1
Đáp án B
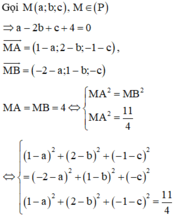
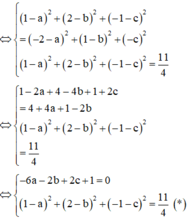


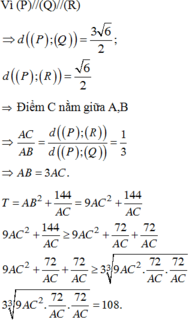
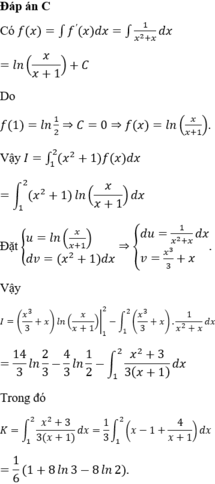
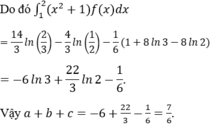
Đáp án D.