Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
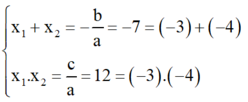
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.

a) x 2 – 7 x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 1 . 12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
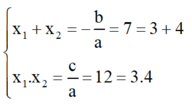
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
b) x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
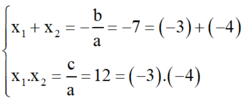
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.

Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
\(x^2_1+x^2_2=\left(x_1+x_2\right)^2-2x_1x_2\\ =\left[\dfrac{-2\left(m-1\right)^2}{7}\right]-2\dfrac{\left(-m\right)^2}{7}\\ =\dfrac{4m^2-8m+4}{49}+\dfrac{2m^2}{7}\\ =\dfrac{4m^2-8m+4+14m^2}{49}\\ =\dfrac{18m^2-8m+4}{49}\)
Vậy \(x^2_1+x^2_2=\dfrac{18m^2-8m+4}{49}\).
Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
x\(\dfrac{1}{2}\)+x\(\dfrac{2}{2}\)=(x1+x2)2−2x1x2
=[\(\dfrac{-2\left(m-1\right)^2}{7}\)]-2\(\dfrac{\left(-m\right)^2}{7}\)
=\(\dfrac{4m^2-8m+4}{49}\)+\(\dfrac{2m^2}{7}\)
=\(\dfrac{4m^2-8m+4+14m^2}{49}\)
=\(\dfrac{18m^2-8m+4}{49}\)
vậy x\(\dfrac{2}{1}\)+x\(\dfrac{2}{2}\)=\(\dfrac{18m^2-8m+4}{49}\)
![]()

\(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}\\x_1x_2=\frac{c}{a}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x_1+x_2=7\\x_1x_2=12\end{cases}\Leftrightarrow}x_{1,2}=3;4\)

a: \(x^2-6x+8=0\)
nên (x-2)(x-4)=0
=>x=2 hoặc x=4
b: \(x^2-12x+32=0\)
nên (x-4)(x-8)=0
=>x=4 hoặc x=8
c: \(x^2+6x+8=0\)
nên (x+2)(x+4)=0
=>x=-2 hoặc x=-4
d: \(x^2-3x-10=0\)
nên (x-5)(x+2)=0
=>x=5 hoặc x=-2
e: \(x^2+3x-10=0\)
=>(x+5)(x-2)=0
=>x=-5 hoặc x=2

a) ta có : \(S=x_1+x_2=\dfrac{7}{2};P=x_1x_2=1\)
b) ta có \(S=x_1+x_2=\dfrac{-9}{2};P=x_1x_2=\dfrac{7}{2}\)
c) ta có : \(S=x_1+x_2=\dfrac{-4}{2-\sqrt{3}};P=x_1x_2=\dfrac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) ta có : \(S=x_1+x_2=\dfrac{3}{1,4}=\dfrac{15}{7};P=x_1x_2=\dfrac{1,2}{1,4}=\dfrac{6}{7}\)
e) ta có : \(S=x_1+x_2=\dfrac{-1}{5};P=x_1x_2=\dfrac{2}{5}\)
a) Theo hệ thức Vi-ét :
x1+x2=\(\frac{-b}{a}=\frac{7}{2}\)
x1x2=\(\frac{c}{a}=\frac{2}{2}=1\)
b) theo hệ thức Vi-ét:
x1+x2=\(\frac{-b}{a}=\frac{-9}{2}\)
x1x2=\(\frac{c}{a}=\frac{7}{2}\)
c)x1+x2=\(\frac{-b}{a}=\frac{-4}{2-\sqrt{3}}=-8-4\sqrt{3}\)
x1x2=\(\frac{c}{a}=\frac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) x1+x2=\(\frac{-b}{a}=\frac{3}{1,4}=\frac{15}{7}\)
x1x2=\(\frac{c}{a}=\frac{1,2}{1,4}=\frac{6}{7}\)
e) x1+x2=\(\frac{-b}{a}=\frac{-1}{5}\)
x1x2=\(\frac{c}{a}=\frac{2}{5}\)
Dùng hệ thức Viet để tính nhẩm các nghiệm của phương trình:
a) x2 - 7x + 12 = 0; b) x2 + 7x+ 12 = 0.

a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = \(-\dfrac{-7}{1}\) = 7 = 3 + 4
x1x2 = \(\dfrac{12}{1}\) = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = \(\dfrac{-7}{1}\) = -7 = -3 + (-4)
x1x2 = \(\dfrac{12}{1}\) = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.
a) x2 – 7x + 12 = 0 có a = 1, b = -7, c = 12
nên x1 + x2 = = 7 = 3 + 4
x1x2 = = 12 = 3 . 4
Vậy x1 = 3, x2 = 4.
b) x2 + 7x + 12 = 0 có a = 1, b = 7, c = 12
nên x1 + x2 = = -7 = -3 + (-4)
x1x2 = = 12 = (-3) . (-4)
Vậy x1 = -3, x2 = -4.

Theo định lý Vi-ét có :
\(\hept{\begin{cases}x_1+x_2=-m\\x_1x_2=-35\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1+x_2=-m\\7\cdot x_2=-35\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1+x_2=-m\\x_2=-5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=-\left(7-5\right)=-2\\x_2=-5\end{cases}}\)
P/s : E mới đọc cái định lý này, sai ở đâu thì mọi người cho e ý kiến với ạ :)) E cảm ơn !!

a) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{-35}{1}=-35\\ \Leftrightarrow7x_2=-35\\ \Leftrightarrow x_2=-5\\ x_1+x_2=\dfrac{-m}{1}=-m\\ \Leftrightarrow7+\left(-5\right)=-m\\ \Leftrightarrow-m=2\\ \Leftrightarrow m=-2\)
b) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-\left(-13\right)}{1}=13\\ \Leftrightarrow12,5+x_2=13\\ \Leftrightarrow x_2=0,5\\ x_1x_2=\dfrac{m}{1}=m\\ \Leftrightarrow12,5\cdot0,5=m\\ \Leftrightarrow m=6,25\)
c) Dùng hệ thức Viét ta có:
\(x_1+x_2=\dfrac{-3}{4}\\ \Leftrightarrow-2+x_2=\dfrac{-3}{4}\\ \Leftrightarrow x_2=\dfrac{5}{4}\\ x_1x_2=\dfrac{-m^2+3m}{4}\\ \Leftrightarrow4x_1x_2=-m^2+3m\\ \Leftrightarrow4\cdot\left(-2\right)\cdot\dfrac{5}{4}+m^2-3m=0\\ \Leftrightarrow m^2-3m-10=0\\ \Leftrightarrow m^2-5m+2m-10=0\\ \Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\\ \Leftrightarrow\left(m+2\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2\\m=5\end{matrix}\right.\)
d) Dùng hệ thức Viét ta có:
\(x_1x_2=\dfrac{5}{3}\\ \Leftrightarrow\dfrac{1}{3}x_2=\dfrac{5}{3}\\ \Leftrightarrow x_2=5\\ x_1+x_2=\dfrac{-\left[-2\left(m-3\right)\right]}{3}=\dfrac{2\left(m-3\right)}{3}=\dfrac{2m-6}{3}\\ \Leftrightarrow3\left(x_1+x_2\right)=2m-6\\ \Leftrightarrow3\left(\dfrac{1}{3}+5\right)=2m-6\\ \Leftrightarrow3\cdot\dfrac{16}{3}+6=2m\\ \Leftrightarrow16+6=2m\\ \Leftrightarrow22=2m\\ \Leftrightarrow m=11\)
x2 – 7x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b2 – 4ac = (-7)2 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.