Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 1 : a) oh là tia đối oz \(\Rightarrow\) zoh thẳng hàng
ot là tia đối của tia ox \(\Rightarrow\) xot thẳng hàng
ta có : xoz = \(\dfrac{100}{2}=50^0\) (oz là tia phân giác của góc xoy)
mà xoz = toh (đối đỉnh) \(\Rightarrow\) toh = 500
b) ta có : toh = xoz (đối đỉnh)
mà toh = 400 \(\Rightarrow\) xoz = 400
\(\Rightarrow\) xoy = 40.2 = 800
bạn ơi tớ bảo phần ab bài 1 tớ biết làm rồi tớ muốn cậu có thể giúp tớ bài 2 và bài 3,bài 1 c,d được không
xin cảm ơn các bạn trước!

a) Số học sinh giỏi toàn diện trong nhóm là:
20 x 3/5 = 12 ( học sinh)
b) Số học sinh của lớp 7A là:
12 : 2/7 = 42 ( học sinh)
* LƯU Ý: Mik thay đổi đề một chút, bởi vì số học sinh của lớp 7A phải bằng 7/2 số học sinh toàn diện.

Gọi số học sinh lớp \(7A;7B;7C\) lần lượt là \(a;b;c\)
Theo đề bài ta có:
\(\dfrac{2}{3}a=\dfrac{3}{4}b=\dfrac{4}{5}c\Leftrightarrow\dfrac{2a}{3}=\dfrac{3b}{4}=\dfrac{4c}{5}\)
Tương đương với:
\(\dfrac{2a}{3}.\dfrac{1}{12}=\dfrac{3b}{4}.\dfrac{1}{12}=\dfrac{4c}{5}.\dfrac{1}{12}\)
\(\Leftrightarrow\dfrac{2a}{36}=\dfrac{3b}{48}=\dfrac{4c}{60}\)
\(\Leftrightarrow\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{15}=\dfrac{a+b-c}{18+16-15}=\dfrac{57}{19}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=18.3=54\\b=16.3=48\\c=15.3=45\end{matrix}\right.\)

B A C M K H G I
a) Xét hai tam giác MHB và MKC có:
MB = MC (gt)
Góc HMB = góc KMC (đối đỉnh)
MH = MK (gt)
Vậy: tam giác MHB = tam giác MKC (c - g - c)
c) Ta có: AM = MB = MC = \(\dfrac{1}{2}\) BC (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
=> Tam giác MAB cân tại M
=> MH là đường cao đồng thời là đường trung tuyến
hay HB = HA
=> CH là đường trung tuyến ứng với cạnh AB
Hai đường trung tuyến AM và CH cắt nhau tại G
=> G là trọng tâm của tam giác ABC
Mà BI đi qua trọng tâm G (G thuộc BI)
Do đó BI là đường trung tuyến còn lại
hay I là trung điểm của AC (đpcm).

Đổi 1/2=2/4
Ta có sơ đồ:
Số học sinh giỏi:/-----/-----/-----/
Số học sinh khá:/-----/-----/-----/-----/ } 45 học sinh
Số học sinh trung bình:/-----/-----/
Tổng số phần bằng nhau:
3+4+2=9 phần
Số học sinh giỏi của lớp đó có là:
45:9x3=15 học sinh giỏi
Số học sinh khá của lớp đó có là:
45:9x4=20 học sinh khá
Số học sinh trung bình của lớp đó có là:
45-15-20=10 học sinh trung bình
Đáp/Số: 15 học sinh giỏi
20 học sinh khá
10 học sinh trung bình

Giải:
Gọi a,b,c,d lần lượt là số hs khối 6,7,8,9 \(\left(a,b,c,d\in N^{sao}\right)\)
Theo đề bài ta có:
\(\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}\) và \(b-d=70\)
Theo tính chất dãy tính số bằng nhau
Ta có: \(\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}=\frac{b-d}{8-6}=\frac{70}{2}=35\)
Từ \(\frac{a}{9}=35\Rightarrow a=315\)
\(\frac{b}{8}=35\Rightarrow b=280\)
\(\frac{c}{7}=35\Rightarrow c=245\)
\(\frac{d}{6}=35\Rightarrow d=210\)
Vậy 315, 280, 245, 210 lần lượt là số hs khối 6,7,8,9

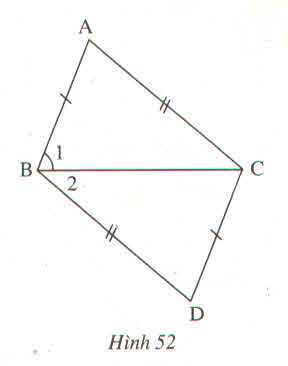
a) Xét t/g MAC và t/g MDB có:
MA = MD (gt)
AMC = DMB ( đối đỉnh)
MC = MB (gt)
Do đó, t/g MAC = t/g MDB (c.g.c) (đpcm)
b) t/g MAC = t/g MDB (câu a)
=> AC = BD (2 cạnh tương ứng) (1)
MCA = MBD (2 góc tương ứng)
Mà MCA và MBD là 2 góc ở vj trí so le trong nên AC // BD (đpcm) (2)
c) Xét t/g ANC và t/g BNE có:
AN = BN (gt)
ANC = BNE ( đối đỉnh)
NC = NE (gt)
Do đó, t/g ANC = t/g BNE (c.g.c)
=> AC = BE (2 cạnh tương ứng) (3)
và ACN = BEN (2 góc tương ứng)
Mà ACN và BEN là 2 góc ở vj trí so le trong nên AC // EB (4)
Từ (2) và (4) => E,B,D thẳng hàng
Từ (1) và (3) => EB = BD
Do đó, B là trung điểm của DE
Dễ thấy, t/g ACE = t/g BEC (c.g.c)
=> CAE = EBC (2 góc tương ứng)
Vậy ta có đpcm

Chọn D