Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có Um không đổi và để UAm luôn không đổ vs mọi gtri của R thì : Um=UAm hay ZL=2ZC =2.100=200 → L=2/π ( D)
Sử dụng hình vẽ suy luận cho nhanh : R ZL ZC UAm Um

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Khi tăng điện dung nên 2.5 lần thì dung kháng giảm 2.5 lần. Cường độ dòng trễ pha hơn hiệu điện thế $\pi/4$ nên
$Z_L-\frac{Z_C}{2.5}=R$
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì $Z_LZ_C=R^2+Z_L^2$
$Z_LZ_C=(Z_L-\frac{Z_C}{2.5})^2+Z_L^2$
Giải phương trình bậc 2 ta được: $Z_C=\frac{5}{4}Z_L$ hoặc $Z_C=10Z_L$(loại vì Zl-Zc/2.5=R<0)
$R=\frac{Z_L}{2}$
Vẽ giản đồ vecto ta được $U$ vuông góc với $U_{RL}$ còn $U_C$ ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi $U_L$ và $U_{LR}$
$\tan\alpha=\frac{R}{Z_L}=0.5$
$\sin\alpha=1/\sqrt5$
$U=U_C\sin\alpha=100V$
\(U_{C}{max}=\frac{U\sqrt{R^{2}+Z_L^{2}}}{R}\); \(Zc=\frac{R^{2}+Z_L^{2}}{Z_L}\)
khi C2=2,5C1---->Zc2=Zc1/2,5=ZC/2,5
do i trể pha hơn U nên Zl>Zc/2,5
\(\tan\frac{\pi }{4}=\frac{Z_L-0,4Zc}{R}=1\Rightarrow R=Z_L-0,4Z_C\)
\(\Rightarrow Z_C.Z_L=Z_L^{2}+(Z_L-0,4Z_C)^{2}\Rightarrow 2Z_L^{2}-1,8Z_CZ_L+0,16Z_C^{2}=0\Rightarrow Z_L=0,8Z_C;Z_L=0,1Z_C\)(loai)
\(\Rightarrow R=Z_L-1,25.0,4Z_L=0,5Z_L\)
\(\Rightarrow U_{C}{max}=\frac{U\sqrt{Z_L^{2}+0,25Z_L^{2}}}{0,5Z_L}=100\sqrt{5}\Rightarrow U=100V\)

Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

Do \(u_L\) vuông pha với \(i\)nên \(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
Khi u cực đại thì \(u=U_0\), thế vào biểu thức trên ta tìm đc i = 0.
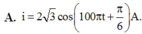
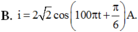
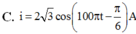
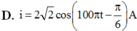
Đáp án C
+ Dung kháng của cuộn dây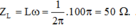
+ Với đoạn mạch chỉ chứa cuộn cảm thuần thì cường độ dòng điện luôn trễ pha 1/2π so với điện áp hai đầu mạch.
Ta có hệ thức độc lập thời gian: