Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhớ biểu thức sau, rất hữu ích khi thi trắc nghiệm
\(W_d=n.W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{n+1}}\)
\(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
\(\Rightarrow F_{dh}=k.\Delta l=k.\dfrac{A}{2}=\dfrac{1}{2}kA\left(N\right)\)
\(F_{dh\left(max\right)}=kA\left(N\right)\)
\(\Rightarrow\dfrac{F_{dh}}{F_{dh\left(max\right)}}=\dfrac{\dfrac{1}{2}kA}{kA}=\dfrac{1}{2}\)

Gọi A là biên độ giao động ta có : kA = 10 N; kA2/2 = 1J => A = 0,2 m = 20 cm
Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp Q chịu tác dụng lực kéo của lò xo có độ lớn \(5\sqrt{3}\)
=> Chu kì giao động của vật T = 0,6s
Quãng đường ngắn nhất đi được là trong 0,4s = \(\frac{2T}{3}\) là s = 3A = 60 cm
Vậy B đúng

Kéo vật từ vị trí cân bằng xuống dưới 3cm thì thả vật ra => \(A = 3cm.\)
Hòn bi thực hiện 50 dao động toàn phần trong 20 s
=> Thời gian thực hiện 1 dao động toàn phần (chính là chu kỳ T) : \(T = \frac{20}{50} = 0,4 s.\)
\(\Delta l\) là độ dãn của lò xo khi ở vị trí cân bằng. Tại vị trí cân bằng: \(P = F_{đh}\)
=> \(mg = k\Delta l=> T = 2\pi \sqrt{\frac{m}{k}} = 2\pi\sqrt{\frac{\Delta l}{g}}.\)
=> \(\Delta l = \frac{T^2.g}{4\pi^2} = \frac{T^2}{4} = 0,04 m = 4cm.\)
Lực đàn hồi cực tiểu khác 0 => \(\Delta l \geq A\) => Lực đàn hồi cực tiểu là \(F_{đhmin}=k(\Delta l -A).\)
=> \(\frac{F_{đhmax}}{F_{đhmin}} = \frac{k(\Delta l +A)}{k(\Delta l -A)} = \frac{\Delta l +A}{\Delta l -A} = \frac{4+3}{4-3}= 7.\)

Độ biến dạng của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=\dfrac{1.10}{100}=0,1m=10cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=10(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2^2+\dfrac{(20\sqrt 3)^2}{10^2}\)
\(\Rightarrow A = 4cm\)
Lực đàn hồi cực đại:
\(F_{dhmax}=k\Delta\ell_{max}=k(\Delta\ell_0+A)=100.(0,1+0,04)=14(N)\)
Lực đàn hồi cực tiểu:
\(F_{dhmin}=k\Delta\ell_{min}=k(\Delta\ell_0-A)=100.(0,1-0,04)=6(N)\)

Đáp án B
Phương pháp: Áp dụng công thức tính lực độ lớn lực đàn hồi cực đại của con lắc lò xo dao động điều hoà theo phương thẳng đứng.
Cách giải:
Vật ở vị trí cân bằng thì lò xo dãn một đoạn ∆l.
Ta có:
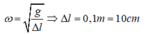
Khi động năng bằng thế năng thì:
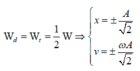
Khi đó:
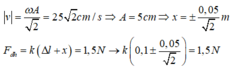
Vì k < 20N/m nên lấy k = 11N/m
Độ lớn cực đại của lực đàn hồi:
![]()

Lực đàn hồi bằng 0 tại li độ \(x=-\Delta\ell_0\)
\(t=\dfrac{7T}{12}\Rightarrow \alpha=\dfrac{7}{12}.360=210^0\)
Biểu diễn dao động bằng véc tơ quay ta có:
30 M N A -A -A/2 x O
Từ hình vẽ dễ dàng ta tìm được: \(\Delta\ell_0=\dfrac{A}{2}\)
Lực đàn hồi cực đại: \(F_{dhmax}=k(\Delta\ell_0+A)=\dfrac{3A}{2}.k\)

Đáp án A