Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
![]() + Lực đàn hồi tác dụng vào con lắc:
+ Lực đàn hồi tác dụng vào con lắc:
![]()
![]()
![]()
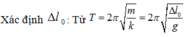
![]()
Như vậy ![]() ứng với vật cách vị trí cân bằng 4cm ở chiều âm.
ứng với vật cách vị trí cân bằng 4cm ở chiều âm.
+ Thời gian ngắn nhất kể từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là:
![]()
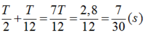

Đáp án B
+ Độ biến dạng của lò xo tại vị trí cân bằng 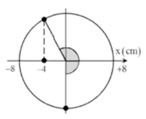
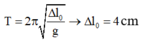
+ Biểu diễn dao động của con lắc tương ứng trên đường tròn.
Lực đàn hồi của lò xo có độ lớn cực tiểu lần đầu tiên khi vật đi qua vị trí lò xo không biến dạng lần đầu, tương ứng với
![]()
→ Từ hình vẽ, ta có
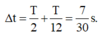

\(\Delta l=5cm\)
Vị trí có lực đẩy đàn hồi lần thứ nhất chính là vị trí lò xo bắt đầu bị nén. Tức là qua vị trí -\(x=-\Delta l\).
M -10 10 N -5 ^
Vị trí ban đầu t = 0 tại M ứng với góc (-90 độ).
Vị trí lực đầy đàn hồi lần thứ nhất tại N x = -5 cm.
=> \(\varphi=\pi+\frac{\pi}{6}=\frac{7\pi}{6}\Rightarrow t=\frac{\varphi}{\omega}=\frac{7\pi}{6.10\pi}=\frac{7}{60}s.\)
sai rồi bạn ơi, lực đẩy max là lúc vật ở vị trí -A nhé, denta phi sẽ là 3π/2, và t sẽ là 3/20s

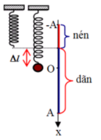


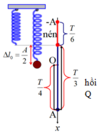
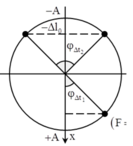
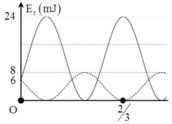

Lực đàn hồi bằng 0 tại li độ \(x=-\Delta\ell_0\)
\(t=\dfrac{7T}{12}\Rightarrow \alpha=\dfrac{7}{12}.360=210^0\)
Biểu diễn dao động bằng véc tơ quay ta có:
30 M N A -A -A/2 x O
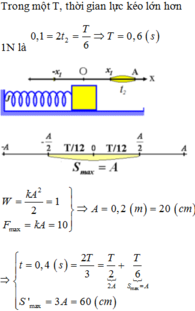
Từ hình vẽ dễ dàng ta tìm được: \(\Delta\ell_0=\dfrac{A}{2}\)
Lực đàn hồi cực đại: \(F_{dhmax}=k(\Delta\ell_0+A)=\dfrac{3A}{2}.k\)