
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

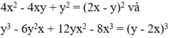

Các bạn nhanh tay giúp mình, mình sẽ tick cho tất cả các câu trả lời nha !
b: \(\dfrac{x^2-2xy+y^2}{x^2-y^2}=\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x-y}{x+y}\)
c: \(\dfrac{2x^2-xy}{2xy-y^2}=\dfrac{x\left(2x-y\right)}{y\left(2x-y\right)}=\dfrac{x}{y}\)
d: \(\dfrac{8-x^3}{x\left(4+2x+x^2\right)}=\dfrac{\left(2-x\right)}{x\left(4+2x+x^2\right)}=\dfrac{2-x}{x}=\dfrac{x-2}{-x}\)

Ta có: \(\frac{x^2y+2xy^2+y^3}{2x^2+xy-y^2}\)
\(=\frac{x^2y+xy^2+xy^2+y^3}{2x^2+2xy-xy-y^2}\)
\(=\frac{xy\left(x+y\right)+y^2\left(x+y\right)}{2x\left(x+y\right)-y\left(x+y\right)}\)
\(=\frac{\left(x+y\right)\left(xy+y^2\right)}{\left(2x-y\right)\left(x+y\right)}=\frac{xy+y^2}{2x-y}\left(đpcm\right)\)
Ta có: \(\frac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}\)
\(=\frac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}\)
\(=\frac{x\left(x+y\right)+2y\left(x+y\right)}{\left(x^2-y^2\right)\left(x+2y\right)}\)
\(=\frac{\left(x+2y\right)\left(x+y\right)}{\left(x+y\right)\left(x-y\right)\left(x+2y\right)}=\frac{1}{x-y}\left(đpcm\right)\)

1) \(VT=x^3+x^2y-x^2y-xy^2+xy^2+y^3=x^3+y^3=VP\)
2) \(VP=x^2+xy-xy-y^2=x^2-y^2=VT\)
3) \(VP=x^2+2\cdot x\cdot1+1=x^2+2x+1=VT\)
4) \(VP=x^3+x^2y+xy^2-x^2y-xy^2-y^3=x^3-y^3=VT\)
1, \(\left(x^2-xy+y^2\right)\left(x+y\right)=x^3+y^3\\ x^3+x^2y-x^2y-xy^2+xy^2+y^3=x^3+y^3\\ x^3+y^3=x^3+y^3\left(đúng\right)\)Vậy ta được đpcm
2, \(x^2-y^2=\left(x-y\right)\left(x+y\right)\\ x^2-y^2=x^2+xy-xy-y^2\\ x^2-y^2=x^2-y^2\left(đúng\right)\)Vậy ta được đpcm
3, \(x^2+2x+1=\left(x+1\right)^2\\ x^2+2x+1=\left(x+1\right)\left(x+1\right)\\ x^2+2x+1=x^2+x+x+1\\ x^2+2x+1=x^2+2x+1\left(đúng\right)\)Vậy ta được đpcm
4, \(x^3-y^3=\left(x-y\right)\left(x^2+xy+y^2\right)\\ x^3-y^3=x^3+x^2y+xy^2-x^2y-xy^2-y^3\\ x^3-y^3=x^3-y^3\left(đúng\right)\)Vậy ta được đpcm

a: \(=\dfrac{4a^2-3a+5}{\left(a-1\right)\left(a^2+a+1\right)}+\dfrac{\left(2a-1\right)\left(a-1\right)}{\left(a-1\right)\left(a^2+a+1\right)}-\dfrac{6a^2+6a+1}{\left(a-1\right)\left(a^2+a+1\right)}\)
\(=\dfrac{4a^2-3a+5+2a^2-3a+1-6a^2-6a-6}{\left(a-1\right)\left(a^2+a+1\right)}\)
\(=\dfrac{-12a}{\left(a-1\right)\left(a^2+a+1\right)}\)
b: \(=\dfrac{5}{a+1}+\dfrac{10}{a^2-a+1}-\dfrac{15}{\left(a+1\right)\left(a^2-a+1\right)}\)
\(=\dfrac{5a^2-5a+5+10a+10-15}{\left(a+1\right)\left(a^2-a+1\right)}\)
\(=\dfrac{5a^2+5a}{\left(a+1\right)\left(a^2-a+1\right)}=\dfrac{5a}{a^2-a+1}\)

\(2005^3-1=\left(2005-1\right)\left(2005^2+2005+1\right)=2004\times\left(2005^2+2005+1\right)⋮2004\left(\text{đ}pcm\right)\)
\(2005^3+125=\left(2005+5\right)\left(2005^2-2005\times5+5^2\right)=2010\times\left(2005^2-2005\times5+5^2\right)⋮2010\)
\(x^6+1=\left(x^2+1\right)\left(x^4-x^2+1\right)⋮x^2+1\left(\text{đ}pcm\right)\)
\(x^6-y^6=\left(x^2-y^2\right)\left(x^4+x^2y^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^4+x^2y^2+y^4\right)⋮x-y;x+y\left(\text{đ}pcm\right)\)

a,(x-y)^2-2(x+y)+1 b, x^2-y^2+4x+4 c, 4x^2-y^2+8(y-2)
=(x-y-1)^2 =(x^2+4x+4)-y^2 =4x^2-y^2+8y-16
=(x+2)^2-y^2 =4x^2-(y^2-8y+16)
=(x+2-y)(x+2+y) =4x^2-(y-4)^2
a) (x+y)2-2(x+y)+1=(x+y-1)2
b) x2-y2+4x+4 = (x2+4x+4)-y2=(x+2)2-y2=(x+y+2)(x-y+2)
c)4x2-y2+8(y-2) = 4x2-(y2-8y+16) = (2x)2-(y-4)2=(2x+y-4)(2x-y+4)
d)x3-2x2+2x-4 = x2(x-2)+2(x-2) = (x-2)(x2+2)
e)xy-4+2x-2y=x(y+2) - 2(y+2) = (x-2)(y+2)

\(P=\left[\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}\right]:\frac{x+1}{2x^2+y+2}\)
\(P=\left[\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{\left(x+y\right)\left(x-2y\right)}\right):\frac{\left(2x^2+y+2\right)\left(2x^2+y-2\right)}{\left(x+y\right)\left(x+1\right)}\right]:\frac{x+1}{2x^2+y+2}\)
\(P=\left(\frac{\left(x-y\right)\left(x+y\right)+x^2+y^2+y-2}{\left(x+y\right)\left(2y-x\right)}.\frac{\left(x+y\right)\left(x+1\right)}{\left(2x^2+y+2\right)\left(2x^2+y-2\right)}\right):\frac{2x^2+y+2}{x+1}\)
\(P=\left(\frac{2x^2+y-2}{2y-x}.\frac{x+1}{2x^2+y-2}\right).\frac{1}{x+1}\)
\(P=\frac{1}{2y-x}\)
Tại \(x=-1,76\) và \(y=\frac{3}{25}\) thì giá trị của \(Q=\frac{1}{2}\)

Chỗ dấu bằng thứ hai sai nên bạn làm cũng chưa đúng
x^6 -y^6 = (x^2-y^2)(x^4 +x^2 .y^2 + y^4)
Bạn hiểu ra chỗ sai của mình chưa.Chúc bạn học tốt.