Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
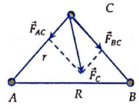
Vì tam giác ABC cân tại C nên ta có AC=BC= R 2
Lực hấp dẫn tác dụng lên chất điểm tại
![]()
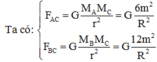
![]()

\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)
\(\overrightarrow{F_D}+\overrightarrow{F_A}+\overrightarrow{F_B}=\overrightarrow{0}\Leftrightarrow F_D^2=F_A^2+F_B^2\)
\(\Leftrightarrow\left(\dfrac{G.m'.m\sqrt{2}}{AD^2}\right)^2=\left(\dfrac{G.m.m'}{AB^2}\right)^2+\left(\dfrac{G.m'.m}{AC^2}\right)^2\)
\(\Leftrightarrow\left(\dfrac{\sqrt{2}}{AD^2}\right)^2=\dfrac{1}{AB^4}+\dfrac{1}{AC^4}\Leftrightarrow\dfrac{2}{AD^2}=\dfrac{1}{a^4}+\dfrac{1}{a^4}=\dfrac{2}{a^4}\)
\(\Rightarrow AD=a^2\)

đổi 500g =0.5kg
<=> Tại điểm thả vật Wo= Wđ +Wt =0 + 0,5.10.45 = 225 (J) (động năng bằng 0)
Sgiây thứ hai= S2s –S2s-1=\(\frac{1}{2}\).10.(22-1)=15(m)
Đây cũng chính là vận tốc vật trong giây thứ 2
Vật rơi ở giây thứ 2 so vơi mặt đất là vị trí A
do bỏ qua ma sát,cơ năng bảo toàn. Áp dụng định luật bảo toàn cơ năng WA = W0
<=> mv2/2 + mgz = 225 (J)
<=> (0,5.152)/2 + Wt =225
<=> Wt = 168,75 (J)
Sgiây thứ hai= S2s –S2s-1=1212.10.(22-1)=15(m)
đoạn này khó hiểu quá

Lần sau tách câu hỏi ra cho dễ nhìn nhé
a/ Tìm M=?m
\(F_{hd1}=\dfrac{Gm_1m'}{r^2};F_{hd2}=\dfrac{Gm_2m'}{r^2};F_{hd3}=\dfrac{Gm_3m'}{r^2}\)
\(\sum\overrightarrow{F}=\overrightarrow{F_{hd1}}+\overrightarrow{F_{hd2}}+\overrightarrow{F_{hd3}}\)
\(\sum\overrightarrow{F}=\overrightarrow{0}\Rightarrow\overrightarrow{F_{hd1}}+\overrightarrow{F_{hd3}}=-\overrightarrow{F_{hd2}}\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{F_{hd13}}\uparrow\downarrow\overrightarrow{F_{hd2}}\left(t/m\right)\\F_{hd13}=F_{hd2}\end{matrix}\right.\)
\(\Rightarrow F_{hd13}=F_{hd2}\Leftrightarrow\sqrt{F_{hd1}^2+F_{hd3}^2+2F_{hd1}.F_{hd3}.\cos\left(\widehat{F_{hd1};F_{hd3}}\right)}=F_{hd2}\)
\(\Leftrightarrow\sqrt{F_{hd1}^2+F_{hd3}^2+2F_{hd1}.F_{hd3}.\cos120^0}=F_{hd2}\)
\(\Leftrightarrow\left(\dfrac{Gm_1m'}{r^2}\right)^2+\left(\dfrac{Gm_3m'}{r^2}\right)^2-\left(\dfrac{Gm_1m'}{r^2}\right).\left(\dfrac{Gm_3m'}{r^2}\right)=\left(\dfrac{Gm_2m'}{r^2}\right)^2\)
\(\Leftrightarrow m_1^2+m_3^2-m_1m_3=m_2^2\Leftrightarrow M^2+m^2-M.m=m^2\)
\(\Leftrightarrow M\left(M-m\right)=0\Leftrightarrow M=m\)
Chọn B.