Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên đường trung tuyến AD có điểm G thỏa mãn: 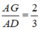
Suy ra: G là trọng tâm tam giác ABC.
Do tia BG cắt AC tại E nên E là trung điểm của AC.
Do tia CG cắt AB tại F nên F là trung điểm của AB.
Theo tính chất trọng tâm tam giác ta có:
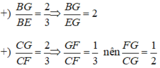
Chọn (B)


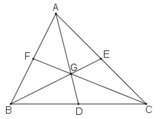
a) Vì G là trọng tâm của \(\Delta ABC\) nên:
\(AF=BF=\dfrac{AB}{2}\)(CG là đường trung tuyến)
\(AE=EC=\dfrac{AC}{2}\) (BE là đường trung tuyến)
mà AB = AC (\(\Delta ABC\) cân tại A)
\(\Rightarrow\) AF = AE
\(\Rightarrow\) \(\Delta AFE\) cân tại A.
Hai tam giác cân AFE và ABC có:
\(\widehat{AFE} = \widehat{ABC}\) \(\left(=\dfrac{180^o-\widehat{BAC}}{2}\right)\)
mà hai góc này ở vị trí đồng vị
\(\Rightarrow\) EF // BC
b) \(\Delta FAM\) và \(\Delta EAM\) có:
AF = AE (cmt)
\(\widehat{FAM}=\widehat{EAM}\) (tính chất tam giác cân)
AM là cạnh chung
\(\Rightarrow\Delta FAM=\Delta EAM\left(c.g.c\right)\)
\(\Rightarrow\) \(\widehat{EMA} = \widehat{AMF}\) (hai góc tương ứng)
\(\Rightarrow\) AM là tia phân giác của \(\widehat{FME}\)
\(\Rightarrow\) G cách đều hai cạnh ME và MF.

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

Bạn tự vẽ hình nha![]()
a.
CE = CA (gt)
=> Tam giác CAE cân tại C
mà ACE = 60
=> Tam giác AEC đều
b.
Tam giác ACE (theo câu a)
=> CAE = 60
Ta có:
BAE + CAE = 90 (2 góc phụ nhau)
BAE + 60 = 90
BAE = 90 - 60
BAE = 30 (1)
Tam giác ABC vuông tại A có:
ABE + ACB = 90
ABE + 60 = 90
ABE = 90 - 60
ABE = 30 (2)
Từ (1) và (2)
=> BAE = ABE
=> Tam giác EBA cân tại E
=> EB = EA
c.
Xét tam giác FAE vuông tại F và tam giác FBE vuông tại F có:
EB = AB (theo câu b)
FBE = FAE (tam giác EBA cân tại E)
=> Tam giác FAE = Tam giác FBE (cạnh huyền - góc nhọn)
=> FB = FA (2 cạnh tương ứng)
=> F là trung điểm của AB
d.
F là trung điểm của AB => EF là trung tuyến của tam giác ABE (3)
I là trung điểm của BE => AI là trung tuyến của tam giác ABE (4)
Từ (3) và (4)
=> G là trọng tâm của tam giác ABE
=> BH là trung tuyến của tam giác ABE
=> H là trung điểm của AE
=> CH là trung tuyến của tam giác CAE đều
=> CH là đường cao của tam giác CAE
hay CH _I_ AE
Chúc bạn học tốt![]()

Chọn C